Nota Para entender este tema, debes estar familiarizado con derivadas, como se explican en el capitulo 3 de Cálculo Aplicado al Mundo Real. Si te gusta, puedes revisar el material del resumen técnicas de diferenciación o, para estudiarlo más detalladamente, el tutorial en rectasobre derivadas de potencias, sumas y múltiplos constantes.

Comencemos con la observación de que si si se acerca en una porción de una curva suave cercano a un punto especificado, se hace indistinguible de la recta tangente en ese punto. En otras palabras:

Por esta razón, la función lineal cuyo gráfica es la recta tangente de y = f(x) en un punto especificado (a, f(a)) se llamada la aproximación lineal de f(x) cercano a x = a.

P ¿Cuál es la fórmula para la aproximación lineal?
R Todo lo que necesitas es la ecuación de la recta tangente en a punto especificado (a, f(a)). Ya que la recta tangente en (a, f(a)) tiene pendiente f'(a), podemos escribir la ecuación utilizando la fórmula punto-pendiente:

y	=	y0 + m(x - x0)
	=	f(a) + f'(a)(x - a)

L(x) = f(a) + f'(a)(x - a).

P El argumento anterior está basado en la geometría: la observación que la recta tangente es indistinguible de la gráfica original cercano al punto de tangencia. ¿Hay una manera algebraica para ver por qué esto es verdad?
R Si. has clic aquí para ver una derivación algebraica de la aproximación lineal.

Aproximación lineal de f(x) cercano a x = a Si x está cercano a a, entonces f(x) ≈ f(a) + (x-a)f'(a). El lado derecho, L(x) = f(a) + (x-a)f'(a), si es una función lineal de x, se llama la aproximación lineal de f(x) cercano a x = a.

 
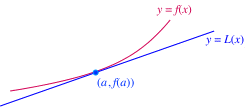
Ejemplo 1 Aproximación lineal de la raíz cuadrada

Sea f(x) = x^1/2. Encuentra la aproximación lineal de f cercano a x = 4 (en el punto (4, f(4)) = (4, 2) en la gráfica), y usa esto aproximadamente √ 4.1.

Solución

f'(x) = 1/(2x^1/2),
f'(4) = 1/(2 ^. 4^1/2) = 1/4.

L(x) = f(4) + (x-4)f'(4)
      = 2 + (x-4)/4
      = 0.25x + 1.

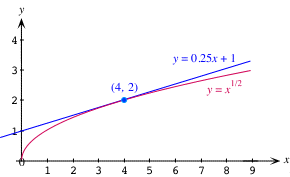
Podemos utilizar L(x) para aproximar la raíz cuadrada de cualquier número cercano a 4 muy fácilmente sin la necesidad de utilizar la calculadora. Por ejemplo,

Ejemplo 2 Aproximación lineal del logaritmo

Utiliza la aproximación lineal para aproximar ln(1.134).

Solución

Aquí, no se nos da un valor para a. La clave es utilizar un valor cercano a 1.134 cuyo logaritmo natura sabemos. Ya que sabemos que ln(1) = 0, tomamos a = 1.

Ahora usa la formula de aproximación lineal:

L(x) = f(a) + (x-a)f'(a).

Sustituyendo y simplificando da (las respuestas numéricas deberían ser exactas a 4 posiciones decimales):

Puedes usar L(x) = x-1 para encontrar aproximaciones para el logaritmo natural de cualquier número cercano a 1: por ejemplo,

ln(0.843) ≈ 0.843 - 1 = -0.157,
ln(0.999) ≈ 0.999 - 1 = -0.001.

Estimación de error

Cuando se hace una medición física, siempre hay cierta incertidumbre respecto a la exactitud. Por ejemplo, si mides el radio de una bola en un rodamiento, puedes medirlo varias veces y obtendrás resultados ligeramente diferentes. En lugar de concluir, por ejemplo, que el radio de la bola es exactamente 1.2mm, puedes mejor concluir que el radio es 1.2 mm ± 0.1 mm. (El cálculo real del rango ± 0.1 mm es frecuentemente dado por una fórmula estadística basada en la derivación estándar de todas las medidas separadas).

Una vez que tengas una estimación del error para el radio, te preguntarás cómo este error podría afectar el cálculo del volumen de la bola. En otras palabras, si el radio es inexacto por 0.1 mm, ¿Por cuánto es inexacto el volumen? Para responder a la pregunta, piensa en el error del radio como un cambio, Δr, en r, y después calcular el cambio asociado, ΔV, en el volumen V. La pregunta general es por lo tanto:

P Si x se cambia por Δx, e y es una función de x, ¿cúal es el cambio asociado Δy en y?

Para responder a esta pregunta, volvemos a la fórmula de la aproximación lineal: Vimos anteriormente que, cercano a x = a,

f(x) ≈ f(a) + (x-a)f'(a),     o
f(x) - f(a) ≈ (x-a)f'(a)

La cantidad f(x) - f(a) representa un cambio en f correspondiente a un cambio en la variable independiente desde a hasta x. En otras palabras,

Cambio en f ≈ Cambio en x × f'(a).

Usando la notación delta, esto se convierte en

Δf ≈ Δx f'(x).

Si y = f(x), escribimos esta fórmula de la siguiente manera

Δy

≈

Δx

dy dx

Observa cómo el dx y Δx aparecerán para cancelar

 
Ejemplo 3 Error de medida

Precisión S.A de C.V. fábrica el rodamiento con bolas de un radio de 1.2 milímetros, que varían por el ±0.1 milímetros. ¿Cúal es el volumen de las bolas, y por cuanto puede variar?

Solución

V	=	4 3	πr3.
dV dr	=	4πr3

Evaluar esta cantidad en r = 1.2 nos da

	V	=	4 3	π(1.2)3	≈	7.24 mm3
dV dr	r=1.2	=	4π(1.2)3		≈	18.10

Por lo tanto,

ΔV

≈

Δr

dV dr

r=1.2

=

(0.1)(18.1) = 1.81

De este modo, el volumen de las bolas es 7.24 ± 1.81 mm³

Ejemplo 4 Pequeños conos

Pequeños Conos Operad S.A. de C.V. fabrica adornos en forma de conos de diferentes colores. Todos los adornos tiene una altura de 10 mm y un radio de la base de 2 mm.

El radio base de los conos es sabido ser exacto hasta 0.15 mm.

(Nota: El volumen de un cono de altura h y radio de base r es

V

=

1 3

πr2h.)

Ahora puedes continuar con los ejercicios para este tema.