|
|||||||||||||
| Matemáticas finitas tema en-línea: regresión lineal y exponencial |
Note: Las matemáticas en esta página han sido mecanografiado por jsMath. Para ver jsMath a su mejor expresión, debe instalar las fuentes jsMath TeX. Haga clic en el botón de jsMath en la parte inferior derecha de la pagina para ver más detalles.
Ya hemos visto como ajustar una recta a un conjunto de dos puntos de datos: Se calcula la ecuación de la recta que pasa por dos puntos dados. (Vea la resumen de funciones para algunos ejemplos.) Sin embargo, por lo general se tiene más que dos puntos de datos, y raras veces están todos en una sola recta. El problema es que hallar la recta que ajusta los datos tan estrechamente que posible.
1. Recta de mejor ajuste (Recta de regresión)
Empezamos intentando construir una función lineal de demanda. Suponga que su investigación de mercado muestra las siguientes estadísticas de venta para casas de varios precios durante el año pasado:
| Precio (Miles de dólares) | $160$ | $180$ | $200$ | $220$ | $240$ | $260$ | $280$ |
| Ventas de nueva casas este año | $126$ | $103$ | $82$ | $75$ | $82$ | $40$ | $20$ |


P ¿Cuál recta ajusta los puntos lo más estrechamente que posible?
R Nos gustaría que las ventas que pronosticara la recta (los valores pronosticados ) estuvieran tan cerca como fuera posible de las ventas reales (los valores observados). Las diferencias entre los valores esperados y los valores pronosticados, que son los errores residuales, son las distancias verticales que se marcan in la figura más abajo.
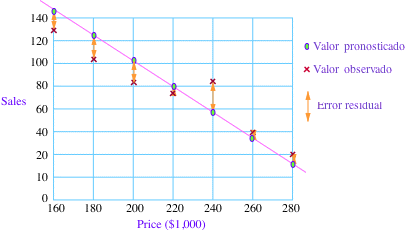
R Sumamos primero todos los cuadrados de los errores residuales para obtener un solo error que se llama el suma de los errores al cuadrado (SSE -- siglas en inglés de "Sum of Squares Error") y escogemos la recta que se da el más pequeño valor de $SSE.$ Esta recta se llama la recta de mejor ajuste, recta de regresión, o recta de mínimos cuadrados asociada a los datos.
 Ejemplo 1: Calculando $SSE$ para una recta dada
Ejemplo 1: Calculando $SSE$ para una recta dada
Supóngase que nos gustaría calcular $SSE$ para una recta especifica, como $y = -x + 300$ como mostrada más abajo:
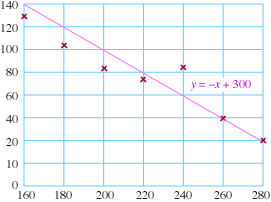
| $SSE$ | $=$ | Suma de los valores de errores residuales |
| $=$ | $- 14 - 17 - 18 - 5 + 22 + 0 + 0 $ | |
| $=$ | $-32$ |
R Presentaremos aquí la formula que la determina. Justificarla necesita cálculo; puede consultar el capitulo de funciones de varias variables en Cálculo Aplicado para una explicación detallada.
Recta de regresión (o mejor ajuste)
La recta que se ajusta mejor a los $n$ puntos $(x_1, y_1),$ $(x_2, y_2),$ $\dots$, $(x_n, y_n)$ tiene la forma
\text{Pendiente} = m = \frac{n\sum xy - \big(\sum x\big)\big(\sum y\big)}{n\sum (x^2) - \big(\sum x\big)^2}
\text{Intersección} = b = \frac{\sum y - m\big(\sum x\big) }{n}
\begin{align*}&\sum xy = \text{ suma del productos }= x_1y_1+x_2y_2 + \dots + x_ny_n\\
&\sum x = \text{ suma del valores de }x = x_1+x_2+\dots +x_n\\
&\sum y = \text{ suma del valores de }y = y_1+y_2+\dots +y_n\\
&\sum x^2 = \text{ suma del valores de }x^2 = x_1^2+x_2^2+\dots +x_n^2\\
\end{align*}
|
El uso de las formulas as bastante fácil, como se muestra el siguiente ejemplo.
 Ejemplo 2: Calculando la recta de regresión a mano
Ejemplo 2: Calculando la recta de regresión a mano
Determine la recta de regresión asociada a los siguientes datos:
| $\pmb x$ | $1$ | $2$ | $3$ | $4$ |
| $\pmb y$ | $1.5$ | $1.6$ | $2.1$ | $3.0$ |
Solución Para aplicar las formulas, es mejor organizar los datos en forma de tabla como sigue: (Cuando ha rellenado los valores de xy y x^2 correctamente, pulse "Sumas" para obtener la suma de cada columna.)
Sustituyendo los valores correctos de la tabla más arriba en las formulas, obtenemos
Por lo tanto, la recta de regresión es
- y = 0.5x + 0.8.
Antes de seguir... Aquí esta una traza de los pontos de dados y la recta de regresión.
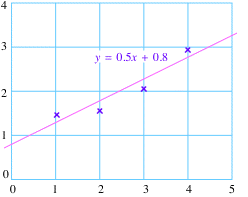
Observe que ni siquiera pasa la recta por uno de los puntos, pero es la recta que se ajusta mejor a los puntos.
Regresamos a los datos sobre la demanda para el mercado de los bienes raíces con la que empezamos este tema.
 Ejemplo 3: Función de demanda
Ejemplo 3: Función de demanda
Obtenga la ecuación de demanda que se ajusta mejor a los siguientes datos, y úsela para pronosticar ventas anuales de casas preciadas a $140,000.
| Precio (Miles de dólares) | 160 | 180 | 200 | 220 | 240 | 260 | 280 |
| Ventas de nueva casas este año | 126 | 103 | 82 | 75 | 82 | 40 | 20 |
Solución Aquí esta una tabla como la que usamos más arriba para organizar las calculaciones:
| \pmb x | \pmb y | \pmb {xy} | \pmb {x^2} |
| 160 | 126 | 20,160 | 25,600 |
| 180 | 103 | 18,540 | 32,400 |
| 200 | 82 | 16,400 | 40,000 |
| 220 | 75 | 16,500 | 48,400 |
| 240 | 82 | 19,680 | 57,600 |
| 260 | 40 | 10,400 | 67,600 |
| 280 | 20 | 5,600 | 78,400 |
| \sum x = 1540 | \sum y = 528 | \sum xy = 107,280 | \sum x^2 = 350,000 |
Sustituyendo estos valores en la formula (con n = 7), obtenemos
Observe que usamos el valor más exacto que pudimos obtener en la calculadora, m \approx -0.7928571429, en lugar del valor redondeado (-0.7929) en la calculación de b. Eso ilustra la sigiuente regla general:
Por lo tanto, la recta de regresión es
Antes de seguir... Más abajo está una traza de la recta de regresión.

P Si mis puntos están en una recta, ¿está la recta de mejor ajuste?
R Sí. Si los puntos están en una recta, el valor mínimo posible de SSE es cero, y eso sucede si se usa la recta que pasa por todos los puntos. Una consecuencia de este hecho es que se puede usar la herramienta regresión en su graficadora o la herramienta regresión en este sitio para calcular la ecuación de la recta que pasa por dos puntos especificados.
P Si no todos los untos están en una recta, ¿cómo puedo saber cuánto se acercan a una recta?
R Hay un número que mide la "bondad de ajuste" de la recta de regresión llamado coeficiente de correlación. Este número, que se representa por r, está entre -1 y 1. Cuanto más se acerca r a -1 o 1, el ajuste es mejor. Si el ajuste es malo, se acerca r a 0. Si el ajusto es exacto, r = -1 para una recta con pendiente negativa, o r = 1 para una recta de pendiente positiva. La figura más abajo muestra varios conjuntos de puntos con sus rectas de regresión, y los valores correspondientes de r.
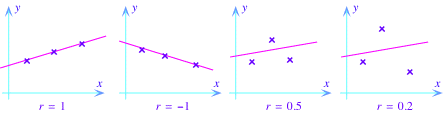
El coefficiente de correlación se puede calcular con la siguiente formula. Para obtener la se requieren buenos conocimientos de estadística.
|
Coeficiente de correlación
\text{Coeficiente de correlación }
= r = \frac{n\bigl(\sum xy\bigr) - \bigl(\sum x\bigr)\bigl(\sum y\bigr)}{\sqrt{n\bigl(\sum x^2\bigr) - \bigl(\sum x\bigr)^2}\cdot \sqrt{n\bigl(\sum y^2\bigr) - \bigl(\sum y\bigr)^2}}
|
2. Curva exponencial de mejor ajuste (Curva exponencial regresión)
P Ahora sabemos como ajustar una recta a un conjunto de datos. ¿Que hay una curva exponencial de la forma
Empiece con la función exponencial
y tome el logaritmo de ambos lados:
Las propiedades de logaritmos nos dan entonces
Esto expresa \log y como una función lineal de x, con
Por lo tanto, si calculamos la recta de mejor ajuste usando \log y como una función de x, entonces la pendiente y la intersección en y serían dados como más arriba, y después podemos obtener los coeficientes r y A por
Para resumir,
|
Regresión exponencial
Para obtener la curva exponencial de mejor ajuste de la forma y = Ar^x
|
 Ejemplo 4: Ventas de Compaq
Ejemplo 4: Ventas de Compaq
Ingresos de ventas de computadores Compaq (una marca ahora extinguida) son mostrados en la siguiente tabla, donde t representa años desde 1990.* Obtenga el modelo exponencial de regresión para los datos.
| \pmb t = Año (1990 = 0) | 0 | 2 | 4 | 7 |
| \pmb R = Ingreso ($ billón) | 3 | 4 | 11 | 25 |
* Datos son redondeados. Fuente: Informes de compañía/The New York Times, Enero 27, 1998, p. D1.
Solución Pues necesitamos modelar \log R como una función lineal de t, primero construimos una tabla con x = t y y = \log R, y entonces calculamos la recta de regresión, y = mx + b.
| \pmb{x\ (= t)} | 0 | 2 | 4 | 7 |
| \pmb{y\ (= \log R)} | 0.477121 | 0.602060 | 1.04139 | 1.39794 |
En lugar de hacer la calculación a mano como hicimos más arriba, podemos utilizar la herramienta regresión en este sitio para hacerlo automáticamente. Simplemente ingrese los valores de x y y y pulse el botón "y = mx+b". (¡Sí, la herramienta puede hacer regresión exponencial directamente, pero preferimos que sabe usted como funciona!)
La recta de regresión que obtenemos es
Por lo tanto, el modelo exponencial deseado es
Nuestra modelo de ingresos es, por lo tanto,
Antes de seguir... Vaya a la herramienta regresión, ingrese los datos originales (sin tomar logaritmos) y pulse el botón "y = a(b^x)". ¿Qué encuentra?
Note: Pues hemos tomado logaritmos antes de hacer la regresión lineal, se puede decir que la curva de regresión exponencial no es la curva que minimiza SSE para los datos originales, esta curva minimiza SSE para los datos tranformados --- es decir, para los datos (x, \log y). Por lo tanto, la curva de regresión exponencial no es la curva exponencial de mejor ajuste en el sentido "estricto." Vea los libros de texto "Applied Calculus" para un método obtener esta curva.
3. Otras formas de regresión
A la herramienta de regresión se puede encontrar también curvas de regresión de las siguientes formas:
En la calculadora TI-83/84, se puede encontrar todos estos y también los siguientes:
Ultima actualización: Enero 2008
Derechos de autor © 2008 Stefan Waner