|
|||||||||||||
| Cálculo aplicado capitulo en-línea: cálculo aplicado a probabilidad y estadística |
| Sección 1. Variables aleatorias continuas e histogramas |
Supóngase que haya comprado acciones en Conglomerado Colosal, S.A., y todos los días note el último precio cotizado de las acciones. El resultado es un número real X (el último precio cotizado de la acción) en el intervalo desacotado [0, +\infty). O bien, supóngase que calcule la duración de un sprint de 50 metros para varios corredores. El resultado para cada corredor es un número real X, el tiempo del carrera en segundos. En ambos casos, el valor de X es bastante aleatorio. Además, X puede tomar su valor en cualquier intervalo en vez de tomar, por ejemplo, solo valores de números enteros. Por esta razón referimos a X como una variable aleatoria continua. La definición formal sigue:
|
Variable aleatoria continua
Una variable aleatoria continua es una función X que asigna a cada resultado posible de un experimento un número real. Si X puede asumir cualquier valor en algun intervalo I (el intervalo puede ser acotado o desacotado), se llama una variable aleatoria continua. Si puede asumir solo varios valores distintos, se llama una variable aleatoria discreta. |
Si X es una variable aleatoria, estamos frecuentemente interesado en la probabilidad de que X asume un valor en cualquier rango. Por ejemplo, si X el último precio cotizado del las acciones de Conglomerado Colosal, y observamos que el precio está entre $10 y $20 60% del tiempo, diríamos
- La probabilidad de que X tome un valor entre $10 y $20 es 0.6.
Escribimos esta declaración matemáticamente como sigue:
 Ejemplo 1 Populación del colegio por edad
Ejemplo 1 Populación del colegio por edad
La siguiente tabla muestra la distribución del residentes estadounidenses (16 años de edad o mayor) quienes asisten a cualquier colegio durante 1980, ordenada por edad:
| Edad | |||||
| Número en 1980 (millones) | 2.7 | 4.8 | 1.9 | 1.2 | 1.8 |
Trace el histograma de la distribución de probabilidad para X = la edad de un universitario elegido al azar..
Solución Antes de empezar, un poco de terminología: Las entradas de la última fila son denominadas como las frecuencias y la tabla como una distribución de frecuencias. Al sumar las frecuencias, observamos que el número total de universitarios durante 1980 fue 12.4 millón. Por lo tanto, podemos convertir todos aquellos datos en probabilidades por dividir entre este total.
| Edad | |||||
| Probabilidad |
Las probabilidades en la tabla más arriba han sido redondeadas, con la consecuencia que suman a 1.01 en vez de lo 1 esperado. In la categoría 15-19, hemos incluido todos de la edad al menos 15 años y menor que 20 años. Por ejemplo, alguien de la edad de 19½ sería incluyendo en este rango. Desearíamos en cambio escribir 15-20, pero esto sería ambiguo, pues no sabríamos donde contar alguien de la edad de precisamente 20 años. Sin embargo, la probabilidad de que un universitario este precisamente de la edad de 20 (y no, por ejemplo, 20 años y 1 segundo) es esencialmente cero, entonces no importa esta ambigüedad (vea el análisis después de Ejemplo 2 más abajo). Por lo tanto, reescribimos la tabla con estos rangos:
| Edad | |||||
| Probabilidad |
La tabla nos informa, por ejemplo, que
- P(15 \leq X \leq 20) = .22
- P(X \geq 35) = .15.
El histograma de la distribución de probabilidad es la gráfica de barras que obtenemos al trazar estos datos:
Antes de seguir... Si hubiera sido más fina la agrupación entre rangos—por ejemplo, con divisiones de 1 año en vez de 5 (y si tuviéramos también los datos anual)—entonces pareciera más pulido el histograma, con barras más bajas como muestra debajo. ¿Porqué?
Esta distribución más pulida sugiera una curva. Este tipo de curva consideraremos en la siguiente sección.
 Ejemplo 2 Edad de un coche alquilado
Ejemplo 2 Edad de un coche alquilado
Una encuesta halla la siguiente distribución de las probabilidades para le edad de un coche alquilado:
| Edad | |||||||
| Probabilidad |
Trace el histograma de la distribución de probabilidad, y úselo para evaluar (o estimar) las siguientes:
-
(a) P(0 \leq X \leq 4)
(b) P(X \geq 4)
(c) P(2 \leq X \leq 3.5)
(d) P(X = 4)

(a) Podemos calcular P(0 \leq X \leq 4) a través de la tabla por sumar las probabilidades correspondientes:
- P(0 \leq X \leq 4) = .20 + .28 + .20 + .15 = .83
Esta probabilidad corresponde a la región sombreada en la siguiente figura:
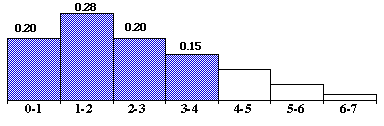
Observe que, pues tiene cada rectángulo una anchura de 1 unidad y una altura igual a la probabilidad asociada, su área es igual a la probabilidad de que X está en el rango asociado. Por lo tanto, P(0 \leq X \leq 4) también es igual a la área de la región sombreada.
(b) De modo parecido, P(X \geq 4) se expresa por la área de la región sin sombra en la figura más arriba, así que
- P(X \geq 4) = .10 + .05 + .02 = .17
(Note que P(0 \leq X \leq 4) + P(X \geq 4) = 1. ¿Porqué?)
(c) Para calcular P(2 \leq X \leq 3.5), tenemos que hacer una conjetura con cierta base, pues no la tabla ni el histograma tiene subdivisiones de anchura 0.5. En referencia al histograma, podemos aproximar la probabilidad por la área mostrada más abajo:
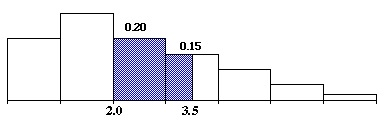
Por lo tanto,
- P(2 \leq X \leq 3.5) \approx .20 + \frac{1}{2}(.15) = .275.
(d) Para calcular P(X = 4), tendríamos que calcular P(4 \leq X \leq 4). Sin embargo, eso correspondería a una región del histograma con cero área (vea la figura más abajo) entonces concluimos que P(X = 4) = 0.
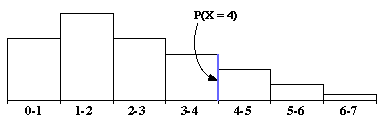
Respuesta Por lo general, sí. Si esta X una variable aleatoria continua, entonces X se puede asumir un número infinito de valores, y por tanto es razonable que la probabilidad de que asuma cualquier solo valor específico es cero.
| Cuidado
Si desee usar un histograma para calcular probabilidad como área, compruebe que los subdivisiones de X tienen anchuras de 1 unidad; por ejemplo, 1 \leq X \leq 2,\ 2 \leq X \leq 3, y así sucesivamente.
El primer histograma en Ejemplo 1 tuvo barras correspondiendo a rangos de X más anchos que 1. La primera barra tiene una anchura de 5 unidades, pues su área es 5 \times .22, que es 5 veces ka probabilidad de que 15 \leq X \leq 20. Si desee usar un histograma para dar probabilidad como área, divida la área por la anchura de los intervalos. |
Hay una otra manera, usada por estadísticos, con la que podemos calcular probabilidad como área en histogramas: Trace su histograma por calcular la altura de cada barra no necesariamente igual a la probabilidad, pero de tal manera que su área es igual a la probabilidad correspondiente.