


 Creating a Family Trust
Creating a Family Trust
 | 2. Probability Density Functions: Uniform, Exponential, Normal, and Beta |  | 3. Mean, Median, Variance and Standard Deviation |  | Calculus and Probability Main Page |  | "Real World" Page |

 Creating a Family Trust
Creating a Family Trust This is not one of those questions that you can answer by consulting a table, so you promise Malcolm an answer by the next day and begin to work on the problem. After a little thought, you realize that the question is one about expected value-the expected future value of an annuity into which monthly payments are made. Since the annuity would terminate upon his death (or his ninety-fifth birthday), you decide that you need a model for the probability distribution of the lifespan of a male in the United States. To obtain this information, you consult mortality tables and come up with the histogram in shown in the following figure (you work with the actual numbers, but they are not important for the discussion to follow).

Next, you decide to model these data with a suitable probability density function. You rule out the uniform and exponential density functions, since they have the wrong shape, and you first try the normal distribution. The normal distribution is


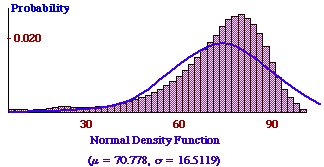
This does not seem like a very good fit at all! Since the actual histogram looks as though it is "pushed over" to the right, you think of the beta distribution, which has that general shape. The beta distribution is given by

Now you just want some function that fits the data. You turn to your statistical software and ask it to find the cubic equation that best fits the data using the least squares method. It promptly tells you that the cubic function that best fits the data is
where
$b = 5.7399145 × 10^{-5}$
$c = -0.0020856085$
$d = 0.0190315095.$
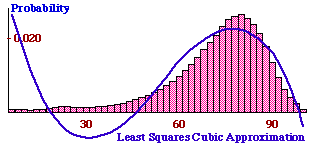
Encouraged, you use the same software to obtain a quartic (degree 4) approximation, and you find:
where
$b = 1.650155×10^{-6},$
$c = -8.523081×10^{-5},$
$d = 0.0016190575$
$e = -0.007865381.$
The following figure shows the result.
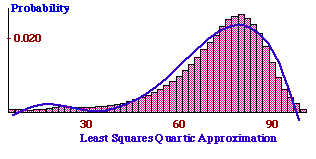
Now that you have the density function you wish to use, you use it to find the expected future value of an annuity into which monthly payments are made. The simplest formula for the future value V of an annuity is
As for the interest rate i, you decide to use a conservative estimate of 5%.
Now the expected value of V(X) is given by
Exercises
1. How much smaller will the payments be if the interest rate is 6%?
2. How much larger would the payments be if Malcolm began payments at the age of 30?
3. Repeat the original calculation using the normal distribution described above. Give reasons for the discrepancy between the answers, explaining why your answer is smaller or larger than the one calculated above.
4. Repeat Exercise 3 using the cubic distribution.
5. If Malcolm wanted to terminate the trust at age $65,$ which model would you use for the probability density? Give reasons for your choice. 6. Suppose you were told by your superior that, since the expected male lifespan is $71,$ you could have saved yourself a lot of trouble by using the formula for the future value of an annuity maturing at age 71. Based on that, the payment comes out to about $$198$ per month. Why is it higher? Why is it the wrong amount?7. Explain how an insurance company might use the above calculations to compute life insurance premiums.

 | 2. Probability Density Functions: Uniform, Exponential, Normal, and Beta |  | 3. Mean, Median, Variance and Standard Deviation |  | Calculus and Probability Main Page |  | "Real World" Page |

Mail us at:
 | Stefan Waner (matszw@hofstra.edu) |  | Steven R. Costenoble (matsrc@hofstra.edu) |