|
If we number the states as 1: Win; 2: Loss; 3: Draw, we get the transition matrix from the given table:
|
This is the one-step transition matrix. To obtain the long-term behavior using technology, we need to compute the matrix P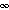 . The rows of P
. The rows of P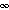 are given by the solution of the following system of equations:
are given by the solution of the following system of equations:
where P is the above transition matrix. This gives the following system of linear equations:
| x + y + z | = | 1 |
| -0.6x + 0.3y + 0.3z | = | 0 |
| 0.4x - 0.6y + 0.3z | = | 0 |
| 0.2x + 0.3y - 0.6z | = | 0 |
Solving the above system gives x = 1/3, y = 10/27, and z = 8/27. P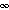 is now the 3
is now the 3 3 matrix whose rows are [ 1/3 10/27 8/27 ]. These three solutions are also the fraction of times England can expect to win, lose, and draw in the long term.
3 matrix whose rows are [ 1/3 10/27 8/27 ]. These three solutions are also the fraction of times England can expect to win, lose, and draw in the long term.
To return to the review exercises, just close this window.