Graphing the Derivative
|
Return to Main Page
Index of On-Line Topics Exercises for This Topic Everything for Calculus Everything for Finite Math Everything for Finite Math & Calculus Utility: Function Evaluator & Grapher Español |
Example 1 Sketching the Graph of the Derivative
Let $f(x)$ have the graph shown below.
Solution
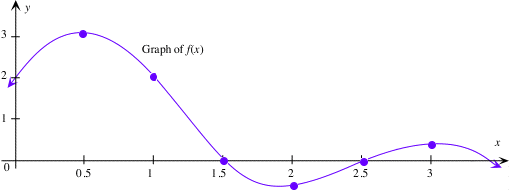
Remember that $f'(x)$ is the slope of the tangent at the point $(x, f(x))$ on the graph of $f.$ To sketch the graph of $f',$ we make a table with several values of $x$ (the corresponding points are shown on the graph) and rough estimates of the slope of the tangent $f'(x).$
| $x$ | $0$ | $0.5$ | $1$ | $1.5$ | $2$ | $2.5$ | $3$ |
| $f'(x)$ | $3$ | $0$ | $-4$ | $-3$ | $0$ | $1$ | $0$ |
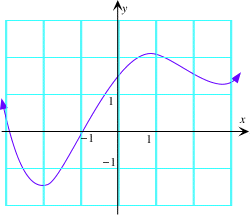
(Note that rough estimates are the best we can do; it is difficult to measure the slope of the tangent accurately without using a grid and a ruler, so we couldn't reasonably expect two people's estimates to agree. However, all that is asked for is a rough sketch of the derivative.) Plotting these points suggests the curve shown below.
Here is a more interactive example.
Example 2 Graph of Derivative
Let $f(x)$ have the graph shown below.
|
Return to Main Page
Index of On-Line Topics Exercises for This Topic Everything for Calculus Everything for Finite Math Everything for Finite Math & Calculus Utility: Function Evaluator & Grapher |