

New Functions from Old:
|
Return to Main Page
Index of On-Line Topics Exercises for This Topic Everything for Calculus Everything for Finite Math Everything for Finite Math & Calculus Utility: Function Evaluator & Grapher |

Let's start by looking at the graphs of some "well-known" functions.

f(x) = x |
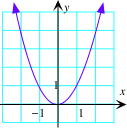
f(x) = x2 |
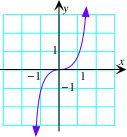
f(x) = x3 |
||||
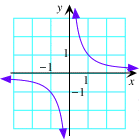
|

f(x) = x1/2 |

f(x) = |x| |
(To review these graphs, consult the section on Functions and Their Graphs in Chapter 1 of Calculus Applied to the Real World)
But what about more complicated functions? For example, what about f(x) = (x-3)2? Notice that here we've taken f(x) = x2 (one of the functions graphed above) and replaced x by (x-3) to get a new function. Well, here are some "shift" rules that tell you the effect of operations like this.
| Rule | Example |
| Horizontal Shift
Let c be a fixed positive number.
|
Here is a picture of the graph of g(x) = |x 4|. It is obtained from the graph of f(x) = |x| by shifting it to the right 4 units. 4|. It is obtained from the graph of f(x) = |x| by shifting it to the right 4 units.
 |
| Vertical Shift
Let c be a fixed positive number.
|
Here is a picture of the graph of g(x) = x2  1. It is obtained from the graph of f(x) = x2 by shifting it down 1 unit. 1. It is obtained from the graph of f(x) = x2 by shifting it down 1 unit.
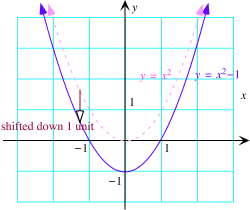 |
Now here is one for you to do.
![]() Example 1 Sketching a Shifted Function
Example 1 Sketching a Shifted Function
| Let f(x) | = | x + 1 | . | Select the correct options and press "Check." |
Now click on the correct graph of the function f.
Here is one that is obtained by two successive translations.
![]() Example 2 Multiple Shifts
Example 2 Multiple Shifts
Let g(x) = (x 2)1/2 + 1. Select the correct options and press "Check."
2)1/2 + 1. Select the correct options and press "Check."
Now click on the correct graph of the function f.
Question: Why does the Horizontal Shift Rule work?
Answer
Question: Why does the Vertical Shift Rule work?
Answer
In addition to the shift rules, we also have the
| Rule | Example |
| Horizontal Scaling
If g(x) = f(cx) with c positive, then:
|
Here is a picture of the graph of g(x) = (0.5x)3. Since c = 0.5 < 1, the graph is obtained from that of f(x) = x3 by stretching it in the x-direction by a factor of 1/c = 2.
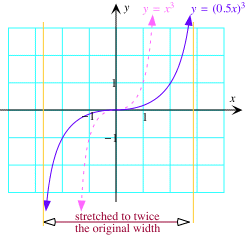 |
| Vertical Scaling
If g(x) = cf(x)with c positive, then:
|
Here is a picture of the graph of g(x) = 3(x)1/2. Since c = 3 > 1, the graph is obtained from that of f(x) = x1/2 by stretching it in the y-direction by a factor of c = 3.
 |
Now one for you.
![]() Example 3 Sketching a Scaled Function
Example 3 Sketching a Scaled Function
| Let g(x) = |
|
|
First graph the function
| f(x) | = |
|
on your graphing calculator (or here) and then click on the correct graph of the function g.
Here is one that is obtained by several successive operations.
| Let g(x) = |
| Select the correct options and press "Check." |
Here are the graphs corresponding to these steps.
| Original Function y = x2 |
Step 1 y = (x  2)2 2)2 |
Step 2
|
Step 3
|
||||||
 |
 |
 |
 |
Finally, we look at reflections.
| Rule | Example |
Horizontal Reflection
(In other words, it "flips it about the y-axis.")
|
Here is a picture of the graph of g(x) =( 0.5x)3+1. It is obtained from the graph of f(x) = 0.5x3+1 by reflecting it in the y-axis. 0.5x)3+1. It is obtained from the graph of f(x) = 0.5x3+1 by reflecting it in the y-axis.
 |
Vertical Reflection
(In other words, it "flips it about the x-axis.") |
Here is a picture of the graph of g(x) =  (x2 (x2  1). It is obtained from the graph of f(x) = x2 1). It is obtained from the graph of f(x) = x2  1 by reflecting it in the x-axis. 1 by reflecting it in the x-axis.
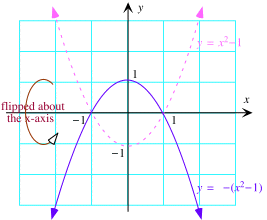 |

|
Return to Main Page
Index of On-Line Topics Exercises for This Topic Everything for Calculus Everything for Finite Math Everything for Finite Math & Calculus Utility: Function Evaluator & Grapher |
