

New Functions from Old:
|
Return to Main Page
Index of On-Line Topics Exercises for This Topic Everything for Calculus Everything for Finite Math Everything for Finite Math & Calculus Utility: Function Evaluator & Grapher Español |

Let's start by looking at the graphs of some "well-known" functions.

$f(x) = x$ |
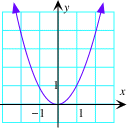
$f(x) = x^{2}$ |
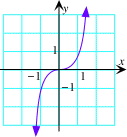
$f(x) = x^3$ |
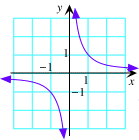
$f(x)=\frac{1}{x}$ |

$f(x) = x^{1/2}$ |

$f(x) = \|x\|$ |
| Rule | Example |
| Horizontal Shift
Let c be a fixed positive number.
|
Here is a picture of the graph of $g(x) = \|x-4\|.$ It is obtained from the graph of $f(x) = \|x\|$ by shifting it to the right $4$ units.
 |
| Vertical Shift
Let c be a fixed positive number.
|
Here is a picture of the graph of $g(x) = x^{2-1}.$ It is obtained from the graph of $f(x) = x^2$ by shifting it down $1$ unit.
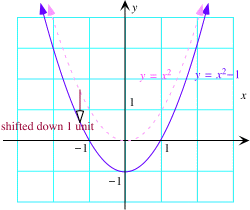 |
Now here is one for you to do.
![]() Example 1 Sketching a Shifted Function
Example 1 Sketching a Shifted Function
Here is one that is obtained by two successive translations.
![]() Example 2 Multiple Shifts
Example 2 Multiple Shifts
Now click on the correct graph of the function $f.$
Question: Why does the Horizontal Shift Rule work?
Answer
Question: Why does the Vertical Shift Rule work?
Answer
In addition to the shift rules, we also have the
| Rule | Example |
Horizontal Scaling
If $g(x) = f(cx)$ with $c$ positive, then:
|
Here is a picture of the graph of $g(x) = (0.5x)^3$. Since $c = 0.5 < 1$, the graph is obtained from that of $f(x) = x^3$ by stretching it in the $x$-direction by a factor of $1/c = 2$.
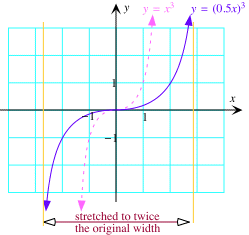 |
Vertical Scaling
If $g(x) = cf(x)$ with $c$ positive, then:
|
Here is a picture of the graph of $g(x) = 3(x)^{1/2}.$ Since $c = 3>1,$ the graph is obtained from that of $f(x) = x^{1/2}$ by stretching it in the $y$-direction by a factor of $c = 3.$
 |
Now one for you.
![]() Example 3 Sketching a Scaled Function
Example 3 Sketching a Scaled Function
Now graph the function
Here is one that is obtained by several successive operations.
Here are the graphs corresponding to these steps.
| Original Function $y = x^2$ |
Step 1 $y = (x-2)^2$ |
Step 2 $y = \frac{(x-2)^2}{3}$ |
Step 3 $y = \frac{(x-2)^2}{3}+4$ |
 |
 |
 |
 |
Finally, we look at reflections.
| Rule | Example |
Horizontal Reflection
|
Here is a picture of the graph of $g(x) = (-0.5x)^{3}+1.$ It is obtained from the graph of $f(x) = 0.5x^{3}+1$ by reflecting it in the $y$-axis.
 |
Vertical Reflection
|
Here is a picture of the graph of $g(x) = -(x^{2} - 1).$ It is obtained from the graph of $f(x) = x^{2} - 1$ by reflecting it in the $x$-axis.
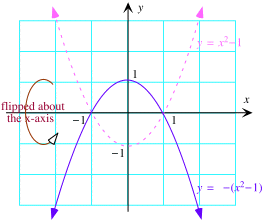 |

|
Return to Main Page
Index of On-Line Topics Exercises for This Topic Everything for Calculus Everything for Finite Math Everything for Finite Math & Calculus Utility: Function Evaluator & Grapher |
