


for
Section 2: Probability Density Functions: Uniform, Exponential, Normal, and Beta
 | Answers to Odd-Numbered Exercises |

In Exercises 19-28, say which kind of probability density function is most appropriate for the given random variable: uniform, exponential, normal, or beta.
20. The time it takes you to drive home
21. The SAT score of a randomly selected student
22. The value of a random number between 0 and 1
23. The time of day at a randomly chosen moment
24. The time it takes a careless driver to be involved in an accident
25. The fraction of fast-food restaurants that are profitable in their first year
26. The time it will take for the sun to die
27. The time it takes before a gambler loses on a bet
28. The length of a 1995 Ford Mustang® tailpipe
Applications
Unless otherwise stated, round answers to all applications to four decimal places.
31. Boring Television Series Your company's new series "Avocado Comedy Hour" has been a complete flop, with viewership continuously declining at a rate of 30% per month. Use a suitable density function to calculate the probability that a randomly chosen viewer will be lost sometime in the next three months.
32. Bad Investments Investments in junk bonds are declining continuously at a rate of 5% per year. Use a suitable density function to calculate the probability that a dollar invested in junk bonds will be pulled out of the junk bond market within the next two years.
33. Radioactive Decay The half-life of Carbon-14 is 5,730 years. What is the probability that a randomly selected Carbon-14 atom will not yet have decayed in 4,000 years' time?
34. Radioactive Decay The half-life of Plutonium-239 is 24,400 years. What is the probability that a randomly selected Plutonium-239 atom will not yet have decayed in 40,000 years' time?
35. The Doomsday Meteor The probability that a "doomsday meteor" will hit the earth in any given year and release a billion megatons or more of energy is on the order of 0.000 000 01.
Source: NASA International Near-Earth-Object Detection Workshop (The New York Times, January 25, 1994, p. C1.)
36. Galactic Cataclysm The probability that the galaxy MX-47 will explode within the next million years is estimated to be 0.0003.
Exercises 37-44 use the normal probability density function and require either the use of technology for numerical integration or a table of values of the standard normal distribution.
![]() 37. Physical Measurements Repeated measurements of a metal rod yield a mean of 5.3 inches, with a standard deviation of 0.1. What is the probability that the rod is between 5.25 and 5.35 inches long?
37. Physical Measurements Repeated measurements of a metal rod yield a mean of 5.3 inches, with a standard deviation of 0.1. What is the probability that the rod is between 5.25 and 5.35 inches long?
![]() 38. IQ Testing Repeated measurements of a student's IQ yield a mean of 135, with a standard deviation of 5. What is the probability that the student has an IQ between 132 and 138?
38. IQ Testing Repeated measurements of a student's IQ yield a mean of 135, with a standard deviation of 5. What is the probability that the student has an IQ between 132 and 138?
![]() 39. Psychology Tests It is known that subjects score an average of 100 points on a new personality test. If the standard deviation is 10 points, what percentage of all subjects will score between 75 and 80?
39. Psychology Tests It is known that subjects score an average of 100 points on a new personality test. If the standard deviation is 10 points, what percentage of all subjects will score between 75 and 80?
![]() 40. Examination Scores Professor Easy's students earned an average grade of 3.5, with a standard deviation of 0.2. What percentage of his students earned between 3.5 and 3.9?
40. Examination Scores Professor Easy's students earned an average grade of 3.5, with a standard deviation of 0.2. What percentage of his students earned between 3.5 and 3.9?
![]() 41. Operating Expenses The cash operating expenses of the regional Bell companies during the first half of 1994 were distributed about a mean of $29.87 per access line per month, with a standard deviation of $2.65. Ameritech Corporation's operating expenses were $28.00 per access line per month. Assuming a normal distribution of operating expenses, estimate the percentage of regional Bell companies whose operating expenses were closer to the mean than those of Ameritech.
41. Operating Expenses The cash operating expenses of the regional Bell companies during the first half of 1994 were distributed about a mean of $29.87 per access line per month, with a standard deviation of $2.65. Ameritech Corporation's operating expenses were $28.00 per access line per month. Assuming a normal distribution of operating expenses, estimate the percentage of regional Bell companies whose operating expenses were closer to the mean than those of Ameritech.
Source: NatWest Securities/Company Reports/ The New York Times, November 22, 1994, p. D1. (The New York Times, January 25, 1994, p. C1.)
![]() 42. Operating Expenses Nynex Corporation's operating expenses were $35.80 per access line per month in the first half of 1994. Referring to the distribution in the previous exercise, estimate the percentage of regional Bell companies whose operating expenses were higher than those of Nynex.
42. Operating Expenses Nynex Corporation's operating expenses were $35.80 per access line per month in the first half of 1994. Referring to the distribution in the previous exercise, estimate the percentage of regional Bell companies whose operating expenses were higher than those of Nynex.
Source: Ibid.
![]() 43. Operating Expenses SBC Corporation (formerly Southwestern Bell) had operating expenses of $27.70 per access line per month in the first half of 1994. Could SBC justifiably claim that its operating expenses were among the lowest 25% of all the regional Bell companies? Explain. (Use the normal distribution of the above exercises.)
43. Operating Expenses SBC Corporation (formerly Southwestern Bell) had operating expenses of $27.70 per access line per month in the first half of 1994. Could SBC justifiably claim that its operating expenses were among the lowest 25% of all the regional Bell companies? Explain. (Use the normal distribution of the above exercises.)
Source: Ibid.
![]() 44. Operating Expenses US West Corporation had operating expenses of $29.10 per access line per month in the first half of 1994. Were US West's operating expenses closer to the mean than those of most other regional Bells? Explain. (Use the normal distribution of the above exercises.)
44. Operating Expenses US West Corporation had operating expenses of $29.10 per access line per month in the first half of 1994. Were US West's operating expenses closer to the mean than those of most other regional Bells? Explain. (Use the normal distribution of the above exercises.)
Source: Ibid.
Cumulative Distribution If f is a probability density function defined on the interval (a, b), then the cumulative distribution function F is given by
 axf(t) dt.
axf(t) dt.
45. Why is F'(x) = f(x) ?
46. Use the result of the previous exercise to show that
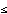 X
X 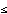 d) = F(d)
d) = F(d)  F(c)
F(c)
for a 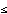 c
c 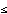 d
d 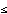 b.
b.
47. Show that F(a) = 0 and F(b) = 1.
48. Can F(x) can have any local extrema? (Give a reason for your answer.)
49-54. Find the cumulative distribution functions for each of the situations described in Exercises 29 through 34.
Communication and Reasoning Exercises
55. Why is a probability density function often more convenient than a histogram?
56. Give an example of a probability density function that is increasing everywhere on its domain.
57. Give an example of a probability density function that is concave up everywhere on its domain.
58. Suppose that X is a normal random variable with mean µ and standard deviation  , and that Z is a standard normal variable. Using the substitution z = (x
, and that Z is a standard normal variable. Using the substitution z = (x  µ)/
µ)/ in the integral, show that
in the integral, show that
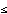 X
X 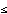 b) =
P[ (a
b) =
P[ (a µ)/
µ)/
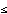 Z
Z 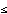 (b
(b µ)/
µ)/ ].
].
59. Your friend thinks that if f is a probability density function for the continuous random variable X, then f(a) is the probability that X = a. Explain to your friend why this is wrong.
60. Not satisfied with your explanation in the previous exercise, your friend then challenges you by asking, "If f(a) is not the probability that X = a, then just what does f(a) signify?" How would you respond?
61. Your friend now thinks that if F is a cumulative distribution function for the continuous random variable X, then F(a) is the probability that X = a. Explain why your friend is still wrong.
62. Once again not satisfied with your explanation in the previous exercise, your friend challenges you by demanding, "If F(a) is not the probability that X = a, then just what does F(a) signify?" How would you respond?

 | Answers to Odd-Numbered Exercises |

 | Stefan Waner (matszw@hofstra.edu) |  | Steven R. Costenoble (matsrc@hofstra.edu) |