Introduction to Logic

In each of the following exercises, supply the missing statement or reason, as the case may be. (To make life simpler, we shall allow you to write ~(~p) as just p whenever it occurs. This saves an extra step in practice.)

	Statement	Reason		Statement	Reason
1.	1. p~q	Premise	2.	1. ~pq	Premise
	2. p	Premise		2. ~p	Premise
	3. - - - -	1,2 Modus Ponens		3. - - - -	1,2 Modus Ponens
3.	1. (~pq) ~(qr)	Premise	4.	1. (~pq)(q~r)	Premise
	2. ~pq	Premise		2. ~pq	Premise
	3. - - - -	1,2 Modus Ponens		3. - - - -	1,2 Modus Ponens
5.	1. (~pq)~(qr)	Premise	6.	1. (~pq)(q~r)	Premise
	2. qr	Premise		2.~(q~r)	Premise
	3. - - - -	1,2 Modus Tollens		3. - - - -	1,2 Modus Tollens
7.	1. ~(~pq)	Premise	8.	~(p~q)	Premise
	2. - - - -	De Morgan		2. - - - -	De Morgan
9.	1. (pr)~q	Premise	10.	1. (~pq)(q~r)	Premise
	2. ~qr	Premise		2. (q~r)s	Premise
	3. - - - -	1,2 Transitive Law		3. - - - -	1,2 Transitive Law
11.	1. (pr)~q	Premise	12.	1. (~pq)(q~r)	Premise
	2. ~qr	Premise		2. (q~r)s	Premise
	3. ~r	Premise		3. ~s	Premise
	4. - - - -	1,2 Transitive Law		4. - - - -	1,2 Transitive Law
	5. - - - -	3,4 Modus Tollens		5. - - - -	3,4 Modus Tollens
13.	1. (pq)r	Premise	14.	1. ~(pq)s	Premise
	2. ~r	Premise		2. ~s	Premise
	3. - - - -	1,2 Disjunctive Syllogism		3. - - - -	1,2 Disjunctive Syllogism
15.	1. p(rq)	Premise	16.	1. (pq)r	Premise
	2. ~r	Premise		2. ~r	Premise
	3. - - - -	2, Addition of ~q		3. - - - -	1,2 Modus Tollens
	4. - - - -	3, De Morgan		4. - - - -	3, De Morgan
	5. - - - -	1,4 Modus Tollens		5. - - - -	Simplification
17.	1. (pq)r	Premise	18.	1. pr	Premise
	2. q	Premise		2. p	Premise
	3. p	Premise		3. s	Premise
	4. - - - -	3,2 Rule C		4. - - - -	1,2 Modus Ponens
	5. - - - -	1,4 Modus Ponens		5. - - - -	3,4 Rule C
19.	1. ~(~pq)p~q	- - - -	20.	1. [(~pq)~q]p	- - - -
21.	1. p~(qr)		22.	1. (st)(q~r)	Premise
	2. qr	Premise		2. (st)	Premise
	3. ~p	- - - -		3. q~r	- - - -
23.	1. ~p(rs)		24.	1. ~pq	Premise
	2. p(rs)			2. ~p~q	- - - -
25.	1. ~[p~(qr)]	Premise	26.	1. (~p~q)p	Premise
	2. ~[~p~(qr)]	- - - -		2. ~(~p~q)p	- - - -
	3. p(qr)	- - - -		3. (pq)p	- - - -
27.	1.(pq)(rs)	Premise	28.	1. (pq)~r	Premise
	2. p	Premise		2. ~p~q	Premise
	3. pq	- - - -		3. ~(pq)	- - - -
	4. rs	- - - -		4. ~r	- - - -
	5. r	- - - -		5. ~rs	- - - -
29.	1. p~q	Premise	30.	1. (pq)(r~s)	Premise
	2. ~q~r	Premise		2. ~rs	Premise
	3. (r~p)t	Premise		3. ~(r~s)	- - - -
	4. p~r	- - - -		4. ~(pq)	- - - -
	5. r~p	- - - -		5. ~p~q	- - - -
	6. t	- - - -		6. ~p	- - - -
31.	1. p~p	Premise	32.	1. ~p	Premise
	2. p	- - - -		2. p	Premise
	3. ~p	- - - -		3. ~p~p	- - - -
	4. ~pq	- - - -		4. p~p	- - - -
	5. pq	- - - -		5. pp	- - - -
	6. q	- - - -		6. ~pp	- - - -
33.	1. p~(~p)	- - - -	34.	1. ~pp	Premise
	2. pp	- - - -		2. t	Premise
	3. ~pp	- - - -		3. t~p	- - - -
	4. (~pp)~q	- - - -		4. ~pt	- - - -
	5. ~p(p~q)	- - - -		5. (~pp)(~pt)	- - - -
	6. ~p(~qp)	- - - -		6. ~p(pt)	- - - -
	7. p(~qp)	- - - -
	8. p(qp)	- - - -

Convert each of the following into a symbolic proof, and supply the justifications for each step.

35. For me to carry my umbrella it is necessary that it rain. When it rains I always wear my hat. Today I did not wear my hat. Therefore, it must not be raining, and so I am not carrying my umbrella.

36. For me to take my umbrella it is sufficient that it rain. For me to wear my hat it is necessary that it rain. I am wearing my hat today. Therefore, it must be raining, and so I must have taken my umbrella.

37.You cannot be both happy and rich. Therefore, you are either not happy, or not rich. Now you do appear to be happy. Therefore, you must not be rich.

38. If I were smart or good-looking, I would be happy and rich. But I am not rich. So it's true that either I'm not happy or I'm not rich. In other words, I am not both happy and rich. Therefore I am not smart or good-looking,. In other words I am not smart and neither am I good-looking. In particular, I am not smart.

39.If interest rates fall, then the stock market will rise. If interest rates do not fall, then housing starts and consumer spending will fall. Now, consumer spending is not falling. So, it's true that housing starts are not falling or consumer spending is not falling; that is, it is false that housing starts and consumer spending are both falling. This means that interest rates are falling, so the stock market will rise.

40. If interest rates or the bond market fall, then the stock market will rise. If interest rates do not fall, then housing starts will fall. Housing starts are rising, so interest rates must be falling. Therefore, it is true that interest rates or the bond market are falling, and so the stock market will rise.

Communication and Reasoning Exercises

41. Complete the following sentence. The Modus Tollens rule of inference says that, if bothandappear on a list of statements known to be true, then we can add.

42. Complete the following sentence. The Modus Ponens rule of inference says that, if bothandappear on a list of statements known to be true, then we can add.

43. Modify Example 5 to produce a proof that uses every type of inference rule we have discussed. (Try replacing q by b and referring to Example 4.)

44. Explain why the following is not a reasonable candidate for a new rule of inference:

A

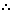AB