The Trigonometric Functions
by
Stefan Waner and Steven R. Costenoble

Answers to Exercises
for
Section 1: Modeling with the Sine Function

1. Modeling with the Sine Function 2. The Six Trigonometric Functions Trigonometric Functions Main Page "RealWorld" Page Everything for Calculus
Return to Exercises

In the following graphs, the first-named function appears in red; the second-named function in yellow.

1.

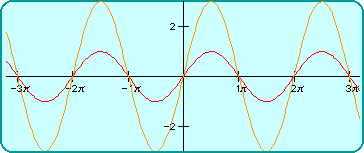
3.

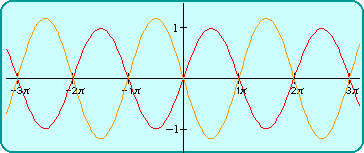
5.

7.

9.

11.

13.

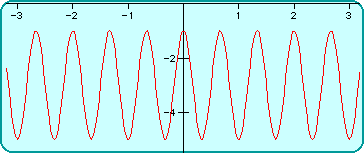
15. $f(x) = 1 + \sin(2\pix)$   17. $f(x) = 1.5\sin(4\pi(x-0.25))$   19. $f(x) = 50\sin(\pi(x-5)/10) - 50$

21. (a) Maximum sales occurred when $t \approx 4.5$ (during the first quarter of 1996). Minimum sales occured when $t \approx 2.2$ (during the third quarter of 1995) and $t \approx 6.8$ (during the third quarter of 1996). (b) Maximum quarterly revenues were $0.561$ billion; minimum quarterly revenues were $0.349$ billion. (c) maximum: $0.455 + 0.106 = 0.561;$  minimum: $0.455 - 0.106 = 0.349$

23. $s(t) = 7.5\sin(2\pi(t-9)/12) + 87.5$

25. $d(t) = 5\sin(2\pi(t-1.625)/13.5)+10$

27. (a) $u(t) = 2.5\sin(2\pi(t-0.75)) + 7.5$    (b) $c(t) = 1.04^t[2.5\sin(2\pi(t-0.75)) + 7.5$

29. Amplitude$= 0.106,$ vertical offset$= 0.455,$ phase shift$= 1.16,$ angular frequency$= 1.39,$ period$= 4.95.$ In 1995 and 1996, quarterly revenue from the sale of computers at Computer City fluctuated in cycles of $4.95$ quarters about a baseline of $0.455$ billion. Every cycle, quarterly revenue peaked at $0.561$ billion ($0.106$ above the baseline) and dipped to a low of $0.349$ billion. During the second quarter of 1995 $(t = 1.16)$ quarterly revenues were was at the baseline level and on an upward cycle.

1. Modeling with the Sine Function 2. The Six Trigonometric Functions Trigonometric Functions Main Page "RealWorld" Page Everything for Calculus
Return to Exercises

We would welcome comments and suggestions for improving this resource. Mail us at:
Stefan Waner (matszw@hofstra.edu) Steven R. Costenoble (matsrc@hofstra.edu)
Last Updated: September, 1996
Copyright © 1996 StefanWaner and Steven R. Costenoble