
The Trigonometric Functions
by
Stefan Waner and Steven R. Costenoble

Exercises
for
Section 1: Modeling with the Sine Function

On the same set of axes, graph the given functions or pairs of functions:
(a) First sketch the curve without any calculator by consulting the discussion in Example 1
 (b) Using graphing technology or a calculator to check your sketches.
(b) Using graphing technology or a calculator to check your sketches.
| 1. $f(t) = \sin(t); g(t) = 3\sin(t)$ |
2. $f(t) = \sin(t); g(t) = 2.2\sin(t)$ |
| 3. $f(t) = \sin(t); g(t) = −1.2\sin(t)$ |
4. $f(t) = \sin(t); g(t) = −2\sin(t)$ |
| 5. $f(t) = \sin(t); g(t) = \sin(t − \pi/4)$ |
6. $f(t) = \sin(t); g(t) = \sin(t + \pi)$ |
| 7. $f(t) = \sin(t); g(t) = \sin(2t)$ |
8. $f(t) = \sin(t); g(t) = \sin(−t)$ |
| 9. $f(t) = 2 − 2\sin(\pit)$ |
10. $f(t) = 3 + 2\sin(\pit)$ |
| 11. $f(t) = 2\sin(3\pi(t−0.5))$ |
12. $f(t) = 2\sin(3\pi(t+1.5))$ |
| 13. $f(t) = 2\sin(3\pi(t−0.5)) − 3$ |
14. $f(t) = 2\sin(3\pi(t+1.5)) + 1.5$ |
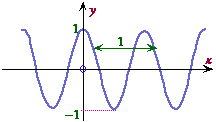
Model each of the following curves with a sine function.
Applications
 21. Computer Sales
21. Computer Sales
Sales of computers are usually subject to seasonal fluctuations. In particular, Computer City's sales of computers in 1995 and 1996 can be approximated by the function
$s(t) = 0.106\sin(1.39t + 1.61) + 0.455$ $(1 ≤ t ≤ 8)$
where $t$ is time in quarters ($t = 1$ represents the end of the first quarter of 1995) and $s(t)$ is computer sales (quarterly revenue) in billions of dollars. †
(a) Use graphing technology to plot sales versus time for the two-year period January 1995 through January, 1997, and use your graph to estimate the value of $t$ and the quarter during which sales were lowest and highest.
(b) Estimate Computer City's maximum quarterly revenue from computer sales.
(c) Indicate how the answers to part (b) can be obtained directly from the the equation for $s(t).$
22. Computer Sales
Repeat Exercise 21 using the following model for CompUSA's quarterly sales of computers: †
$s(t) = 0.0778\sin(1.52t + 1.06) + 0.591$
† The model is based on a regression of data which appeared in The New York Times, January 8, 1997, p. D1. Constants are rounded to three significant digits.
23. Sales Fluctuations
Sales of General Motors cars and light trucks in 1996 fluctuated from a high of $95$ billion in October $(t = 0)$ to a low of $80$ billion in April $(t = 6).*$ Construct a sinusoidal model for the montly sales $s(t)$ of General Motors.
* These are rough figures based on the percentage of the market held by GM as published in The New York Times, January 9, 1997, p. D4.
24. Seasonal Fluctuations
Sales of Ocean King Boogie Boards fluctuate sinusiodally from a low of $50$ units per week each February 1 $(t = 1)$ to a high of $350$ units per week each August 1 $(t = 7).$ Model the weekly sales $s(t)$ of Ocean King Boogie Boards, where $t$ is time in months.
25. Tides
The depth of water at my favorite surfing spot varies from $5$ ft to $15$ ft, depending on the time. Last Sunday, high tide occurred at 5:00 am. and the next high tide occurred at 6:30 pm. Obtain a model to describe the depth of water as a function of time t in hours since midnight on Sunday morning.
26. Tides
Repeat Exercise 25 using data from the depth of water at my other favorite surfing spot, where the tide last Sunday varied from a low of $6$ ft at 4:00 am to a high of $10$ ft.at noon.
27. Inflation
The uninflated cost of Dugout brand snow shovels currently varies from a high of $10$ on January 1 $(t = 0)$ to a low of $5$ on June 1 $(t = 0.5).$
(a) Assuming this trend were to continue indefinitely, calculate the uninflated $cost u(t)$ of Dugout snow shovels as a function of time $t$ in years.
(b) Assuming a $4%$ annual rate of inflation in the cost of snow shovels, the cost of a snow shovel $t$ years from now, adjusted for inflation, will be $1.04^t$ times the un-inflated cost. Write down the cost $c(t)$ of Dugout snow shovels as a function of time $t.$
28. Deflation
Sales of my exclusive 1997 vintage Chateau Petit Mont Blanc vary from a high of 10 bottles per day on April 1 $(t = 0.25)$ to a low of 4 bottles per day on October 1.
(a) Assuming this trend were to continue indefinitely, calculate the undeflated sales $u(t)$ of Chateau Petit Mont Blanc as a function of time t in years.
(b) Regrettably, ever since that undercover expose of my wine-making process, sales of Chateau Petit Mont Blanc have been declining continuously at an annual rate of $12%.$ Using the preseeding exercise as a guide, write down a model for the deflated sales $s(t)$ of Chateau Petit Mont Blanc $t$ years from now.
29. Computer Sales (Based on Exercise 21, but no graphing calculator required)
Computer City's sales of computers in 1995 and 1996 can be approximated by the function
$s(t) = 0.106\sin(1.39t + 1.61) + 0.455$ $(1 ≤ t ≤ 8)$
where $t$ is time in quarters ($t = 1$ represents the end of the first quarter of 1995) and $s(t)$ is computer sales (quarterly revenue) in billions of dollars.† Calculate the amplitude, the vertical offset, the phase shift, the angular frequency, and the period, and interpret the results.
30. Computer Sales
Repeat Exercise 29 using the following model for CompUSA's quarterly sales of computers: †
$s(t) = 0.0778\sin(1.52t + 1.06) + 0.591$
† Source: See Exercise 21.
Communication and Reasoning Exercises
31. If sales of a commodity fluctuate on a seasonal basis with a period of one year, what units of time would give you a simple-looking function?
32. When are the seasonal highs and lows for sales of a commodity modeled by a function of the form $s(t) = A\sin(2\pit) + B$ ? ($A, B$ constants)
33. Your friend has come up with the following model for choral society tupperware stock inventory: $r(t) = 4\sin(2\pi(t−2)/3) + 2.3,$ where $t$ is time in weeks and $r(t)$ is the number of items in stock. Comment on the model.

 | Answers to Odd-Numbered Exercises |

We would welcome comments and suggestions for improving this resource. Mail us at:
 | Stefan Waner (matszw@hofstra.edu)
|  | Steven R. Costenoble (matsrc@hofstra.edu)
|
Last Updated: September, 1996
Copyright © 1996 StefanWaner and Steven R. Costenoble











![]() (b) Using graphing technology or a calculator to check your sketches.
(b) Using graphing technology or a calculator to check your sketches.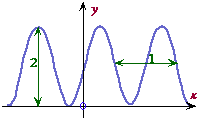
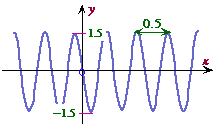

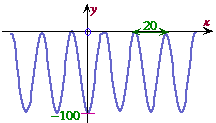
![]() 21. Computer Sales
21. Computer Sales









