6.3 The Definite Integral: Numerical and Graphical Approaches

(This topic is also in Section 6.3 in Applied Calculus and Section 13.3 in Finite Mathematics and Applied Calculus)

Goodies

	Numerical Integration Utility			Excel Riemann Sum Grapher
	Graphing Calculator Programs			Online Text: Numerical Integration

In the textbook we consider an example (Example 1) based in which you are given the marginal cost of making a cell phone call and need to compute the total cost of a two hour call. Instead of going over the same example here, we look at a slightly different scenario here:

The Main Example: A pump is delivering water into a tank at a rate of

where t is time in minutes since the pump is turned on. What is the total amount of water pumped into the tank in the first two minutes?

First Rough Calculation: Since r(t) is the number of liters per minute at which water is entering the tank, when the pump is turned on, this rate is

so the total amount of water pumped into the tank in the first two minutes should be about:

Total amount pumped in	=	Number of liters/minute × Number of Minutes
	=	r(0) × 2
	=	5 × 2 = 10 liters

Here is a graph showing that calculation we just did:

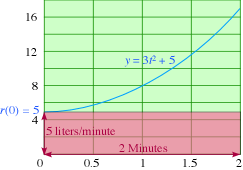Total amount pumped in = 5 liters/minute × 2 Minutes

Notice two things:

The estimated amount pumped in equals the area of the red rectangle.
We have seriously underestimated the amount pumped in because, as the graph shows, the rate at which water is being pumped in increases as time goes on. For instance, at the start of he second minute, the rate is

Referring t the second point above, the reason that we have underestimated the total amount pumped in is that we used the initial rate r(0) throughout the entire 2-minute period.

Let us now redo the calculation using a minute-by-minute calculation, using the rate at the start of each minute for the calculation for that minute:

Minute 1: Total amount pumped in	=	Number of liters/minute at the start of minute 1 × Number of Minutes
	=	r(0) × 1
	=	5 × 1 = 5 liters

This gives a more accurate estimate of the total amount pumped in as

Total for Minute 1 + Total for Minute = 5 + 8 = 13 liters

The new calculation is shown in the following graph:

Minute 1: 5 liters/minute × 1 Minute = 5 liters
Minute 2: 8 liters/minute × 1 Minute = 8liters

Notice that the new estimate is given by the sum of the areas of the two red rectangles.

But wait! This answer is still not exact: For instance, during Minute 1, the rate does not remain constant at 5 liters/minute, but is increasing there as well, and during the second minute, the rate is not constant at 8 liters/minute either. So we will next compute a more accurate third answer by using half-minute by half-minute calculations. But before we go on, let is write down what we have computed using Δt to denote the length of time we use in each step of the computation:

First Calculation (Δt = 2):	r(0)Δt = 5×2 = 10 liters
Second Calculation (Δt = 1):	r(0)Δt + r(1)Δt = 5×1 + 8×1 = 13 liters
Thied Calculation (Δt = 0.5):	r(0)Δt + r(0.5)Δt + r(1)Δt + r(1.5)Δt = 5×0.5 + 5.75×0.5 + 8×0.5 + 11.75×0.5 = 15.25 liters

Each of these calculations is called a left Riemann sum of the function r(t); the first calculation is a Riemann sum with 1 subdivision, the second a Riemann sum with 2 subdivisions, and the third Riemann sum with 4 subdivisions.

Here is the graph for the third calculation:

Riemann Sum with 4 subdivisions:
r(0)Δt + r(0.5)Δt + r(1)Δt + r(1.5)Δt = 15.25 liters

To compute the Riemann sum with 5 subdivisions, use rectangles of width

Δt =

Now we calculate the height of each rectangle:

The height of the first rectangle is	r() =
The height of the second rectangle is	r() =
The height of the third rectangle is	r() =
The height of the fourth rectangle is	r() =
The height of the fifth rectangle is	r() =

To obtain the Riemann sum, we add the areas of all five rectangles. The area of each rectangle is its height times its width Δt (0.4). Instead of multiplying each height by 0.4 and then adding, we can equivalently add the heights and multiply the sum by 0.4:

If you want to see Riemann sums graphically for different numbers of subdivisions, go to the Excel Riemann Sum Grapher, make sure that macros are enabled in Excel (If your Excel security is set to "high," macros will be automatically disabled and the utility will not work, so you will have to reset the security to "medium" through the "Tools" menu in Excel and then relaunch Excel.) Enter 3*x^2+5 in the Function box, set "a" and "b" to 0 and 2 respectively, and choose the number of subdivisions you want to use.

Riemann Sum

If f is a function defined on the interval [a, b] and n is a number (of subdivisions), we define the associated left Riemann sum with n equal subdivisions as follows:

Subdivide the interval [a, b] into n equal intervals of width Δx = (b - a)/n.
Start with x₀ = a and successively add Δx to get additional points

x₁ = x₀ + Δx;
x₂ = x₁ + Δx;
...
x_n-1 = x_n-2 + Δx.
Calculate [f(x₀) + f(x₁) + f(x₂) + ... + f(x_n-1)]Δx
This is the desired Riemann sum.

Examples

We just calculated several Riemann sums for the function f(x) = 3x² + 5 (although we used different letters for the name of the function and the independent variable.) Check to see how the calculations we did match the formula above.
Let f(x) = x², and let [a, b] = [-1, 1]. The Riemann sum for n = 4 subdivisions is calculated as follows:
- Δx =
- x₀ =
  x₁ =
  x₂ =
  x₃ =
- Riemann Sum =

Let us go back to thinking about the Main Example of water being pumped into a tank.

Q None of the Riemann sums we calculated for the water being pumped into the tank gave the right answer; in fact all these calculations ignore the fact that the rate keeps increasing over each interval, so Riemann sums are a waste of time, right?
A The first claim is right, but the second claim is not: Each calculation gives us a more accurate estimate of the amount of water pumped in, and in fact we have discovered an astounding fact:

The exact amount of water pumped in is: (There are two correct answers. Try to click on the two correct ones in succession.)

	A Riemann sum
	The limit of the Riemann sums as the number of subdivisions n → ∞
	The exact area under the curve y = 3t² + 5 above the interval [0, 2]
	Approximately but not exactly the area under the curve y = 3t² + 5 above the interval [0, 2]
	A very large Riemann sum
	Infinite
	More than the area under the curve y = 3t² + 5 above the interval [0, 2]
	Get me out of here!

We have a name for this limit of the Riemann sums or, equivalently, the area under a curve above an interval:

Definite Integral

If f is a function defined on the interval [a, b] then the definite integral of f over [a, b] is defined to be the limit of the Riemann sums as the number of subdivisions n → ∞, assuming the limit exists. We use the following notation for the definite integral:

Definite Integral of f over [a, b]

Limit of Riemann Sums as n → &infin

b

a

f(x) dx

Definite integral, from a to b, of f(x) with respect to x

Geometrically, the definite integral measures area. If the graph of the function is above the x-axis, the area is counted as positive (like the examples we have been looking at). If the graph of the function is below the x-axis, the area is counted as negative. The following picture illustrates the general case:

b

a

f(x) dx

Area A - Area B

Interpretation of the Definite Integral

If f is the rate of change of a quantity F (that is, f = F'), then

b

a

f(x) dx

is the (exact) total change of F from x = a to x = b.

Examples

We can sometimes calculate the definite integrqal geometrically by calculating the area under the curve directly as the following examples show:

3

1

2 dx

3

1

(1+x) dx

4

0

f(x) dx

Q What about areas that are not easy to calculate geomterically?
A The Funcdamental Theorem of Calculus (next section) tells us how to calculate these using antiderivatives. Otherwise, we can alsways use the numerical integration utility to calculate Riemann sums for larger and larger numbers of subdivisions to estimate the integral, as we will in the next example:

A projectile has velocity v(t) = 300 + 5t - 10t² m/s after t seconds after being fired. Use Riemann sums for several values of n to estimate the total distance covered by the projectile from time t = 2 seconds to time t = 4 seconds.

Q How on earth am I supposed to find the distance covered knowing only the (varying) speed?
A Think for a moment about the pump example with which we started: We discovered that:

The total amount of water pumped in over the interval [0, 2] equals the definite integral of the rate from 0 to 2.

More generally, we have (see the "Interpretation" in the above box):

The total change in F over the interval [a, b] equals the definite integral of the rate of change of F from a to b.

In the situation we have here, the velocity v(t) is rate of change of position. So, the total change in position over the interval [2, 4] is

Distance covered = Total change in position

4

2

v(t) dt

Distance covered = Integral of velocity with respect to t

Since v(t) = 300 + 5t - 10t², we have to compute

4

2

(300 + 5t - 10t²) dt,

which can do numerically using the numerical integration utility.

To use the utility, click on the above link, enter the function 300 + 5x - 10x^2 in the "f(x) = " box, enter 2 and 4 in the "Left End-Point" and "Right End-Point" boxes respectively, and try various values of n in the "Number of subdivisions" box. Then press "Left Sum" to get the left Riemann sum.

You now have several options

Try some of the questions in the true/false quiz (warning: it covers the whole of Chapter 6) by pressing the button on the sidebar.
Try some of the on-line review exercises (press the "Review Exercises" button on the side. Again, these questions cover the whole chapter, but you should now be able to answer R1 through R6 and some of the "Apps".)
Try the exercises from Section 6.3 in Applied Calculus or Section or Section 13.3 of Finite Mathematics and Applied Calculus.

Top of Page

Minute 2: Total amount pumped in	=	Number of liters/minute at the start of minute 2 × Number of Minutes
	=	r() ×
	=	× = liters