
| This tutorial: Part A: Variance and Standard Deviation of a Set of Scores |
| Next tutorial: Part B: Variance and Standard Deviation of a Random Variable |

Consider the following two sets of scores:
 |
Set 1 | Set 2 |
Q How do we measure the dispersion of a set of scores?
A Here's how to do it graphically: First, measure the distance of each point from the mean, square each distance, and then take the average of all those squared distances. This measurement is called the population variance of the set of scores.
 |
Sum of squared distances:
102 + 02 + 102 + 102 + 10 2 + 02 = 400 Population variance: 400/6  66.67 66.67
|
Sum of squared distances:
502 + 502 + 252 + 252 + 30 2 + 302 = 8050 Population variance: 8050/6  1341.67 1341.67
|
|
Q Is there a formula to measure this?
A Actually, there are a couple. First, notice that the distance of a typical score x to the mean is given by subtracting it from the mean: x - . Therefore, the square distance is (x -
)2. Then we can get the average of these (the population variance) by adding and dividing by the number of points.
|
Population Variance and Standard Deviation
The population variance (it is written as
The population standard deviation is the square root of the population variance, and is written as
Example
Here is one for you to try. The values you enter must be accurate to 4 dcimal places: |
Q Why do we divide by n when computing the variance and standard deviation for a population, but by n-1 when doing it for a sample?
A When we have a sample, we do not have all the data in the population, but we would still like the sample variance to approximate the population variance. We can interpret this to mean that we would like the average of a very large number of calculations of sample variances for different samples to be very close to the population variance. It turns out that the formula for s2 given above is the formula that accomplishes this task. The sample variance s2 as we have defined it is referred to by statisticians as an "unbiased estimator" of the population variance  2; if, instead, we divided by n in the formula for s2, we would, on average, tend to underestimate the population variance. (See the on-line text on Sampling Distributions for more discussion of unbiased estimators.)
2; if, instead, we divided by n in the formula for s2, we would, on average, tend to underestimate the population variance. (See the on-line text on Sampling Distributions for more discussion of unbiased estimators.)
A Tabular Method for Calculation of Variance & Standard Deviation
Here is a nice way or organizing the data we used in computing the variance and standard deviation of the sample 1, -1, 2, 3:
| x | x - x | (x - x)2 |
| 1 | 1 - 1.25 = -0.25 | (-1.25)2 = 0.0625 |
| -1 | -1 - 1.25 = -2.25 | (-2.25)2 = 5.0625 |
| 2 | 2 - 1.25 = 0.75 | 0.752 = 0.5625 |
| 3 | 3 - 1.25 = 1.75 | 1.752 = 3.0625 |
| 5 | 0 | 8.75 |
 2.91667
2.91667
Q OK. We know how to calculate the standard deviation, which is a measure of dispersion. Is there anything more specific that it tells us?
A There are two ways we can use the standard deviation to get specific information about a set of scores. One of these ways, called the empirical rule, (see blow) gives us a great deal of information, but only applied to distributions of scores that are both bell-shaped and symmetric.
Q What does it mean for a distibution of scores to be bell-shaped?
A It means that if you group the scores into suitable measurement classes (see the tutorial for Section 8.1) and then graph the frequencies or probabilities, you get a nice bell-shaped symmetric curve:
 |
 |
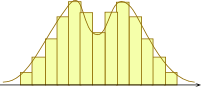 |
Bell-shaped and symmetric | Not symmetric | Not bell-shaped |
|
Empirical Rule
For a set of data whose frequency distribution is bell-shaped and symmetric, the following is true:
Examples 1. If the mean of a sample with a bell-shaped symmetric distribution is 20 with standard deviation s = 2, then approximately 95% of the scores lie in the interval [20-2(2), 20 + 2(2)] = [16, 24]. In other words, approximately 95% of the scores lie between 16 and 24. Note that this also means that approximately 5% of the scores lie outside this range: approximately 2.5% are above 24 and approximately 2.5% are below 16 (since the distribution is symmetric.) |
Q The Empirical Rule rtells us how to interpret the sandard devaition for bell-shaped symmetric distributions. What about distributions that re not bell-shaped and symmetric?
A In cases where the distribution is not nice, we cannot be nearly so accurate. What we can always say is the following:
A
|
Chebyshev's Rule
For an arbitrary set of data (not necessarily bell-shaped or symmetric) the following is true:
Examples 1. If the mean of a sample is 20 with standard deviation s = 2, then at least 3/4, or 75%, of the scores lie in the interval [20-2(2), 20 + 2(2)] = [16, 24]. In other words, approximately 95% of the scores lie between 16 and 24. Note that this also means that at most 25% of the scores lie outside this range. We cannot say that at most 12.5% are above 24 and at most 12.5% below 16 unless we know that the distribution is symmetric. |
Now try some of the exercises in Section 8.4 of Finite Mathematics and Finite Mathematics and Applied Calculus. However, to be able to do all the exercises, you will need to go on to the next tutorial, which deals with random variables rather than sets of scores.
