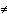Proof

Inverting s(t) requires s'(t) 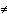0. But, by the Fundamental theorem of Calculus and the definition of L(a, t),

ds dt

2

=

± gij

dxi dt

dxj dt

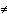0

for all parameter values t. In other words,

dxi dt

,

dxj dt

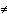0

But this is the "never null" condition which we have assumed. Also,

	dxi ds	,	dxj ds		=	gij dxi ds dxj ds = gij dxi ds dtj ds dt ds 2
					=	±1 ds dt 2     dt ds 2     = ±1.

For the converse, we are given a parameter t such that

dxi dt

,

dxj dt

=

±1.

In other words,

gij

dxi dt

dxj dt

=

±1.

But now, with s defined to be arc-length from t = a, we have

ds dt

2

=

± gij

dxi dt

dxj dt

=

+1.

(the signs cancel for time-like curves) so that

ds dt

2

=

1,

meaning of course that t = ±s + C.

Just close this window to return to the lecture.