Proof that the first curvature vector P of a curve C is at right angles to C

First, some notation: write T_,a for the (ordinary) partial derivative of the tensor T with respect to x^a. This will avoid a lot of messy notation (as if there is not enough already!).

To show the result, we compute

P, T	=	P, dx/ds
	=	Pi dxj ds gij	(Definition of the inner product)
	=	d2xi ds2 + i p q 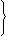dxp ds dxq ds dxj ds gij	(Definition of Pi)
	=	d2xi ds2 + 1 2 gli [gql,p + glp,q - gpq,l] dxp ds dxq ds dxj ds gij
	=	d2xi ds2 dxj ds gij + 1 2 [gqj,p + gjp,q - gpq,j] dxp ds dxq ds dxj ds
		(since gligij = jl)

Looking at the term on the right, we distribute to get 3 terms of the form

gqj,p

dxp ds

dxq ds

dxj ds

=

dgqj ds

dxq ds

dxj ds

by the chain rule,

and we notice that the other two terms are identical to this (except for dummy variables). Thus, we are left with

	d2xi ds2 dxj ds gij + 1 2 dgqj ds dxq ds dxj ds
=	1 2 d ds dxi ds dxj ds gij	(by symmetry of the gij)
=	1 2 d ds T, T	(definition of the inner product)
=	1 2 d ds ( ±1)	(refer back to the Proof of 5.5 to check this)
=	0,

as asserted.

Just close this window to return to the lecture.