 -,-
-,- is an inner product on the vector space L, then there exists a basis {V(1), V(2), . . . , V(n)} for L such that
is an inner product on the vector space L, then there exists a basis {V(1), V(2), . . . , V(n)} for L such that
Proof of Existence of Locally Inertial Frames
This is my own version of the proof. There is a version in Bernard Schutz's book, "A First Course in General Relativity" (Cambridge University Press) but the proof there seems overly complicated and also has some gaps relating to consistency of the the systems of linear equations he sets up.
First, we need a fact from linear algebra: if  -,-
-,- is an inner product on the vector space L, then there exists a basis {V(1), V(2), . . . , V(n)} for L such that
is an inner product on the vector space L, then there exists a basis {V(1), V(2), . . . , V(n)} for L such that
 V(i), V(j)
V(i), V(j) = ±
= ± ij
ij
(To prove this, use the fact that any symmetric matrix can be diagonalized using a P-PT type operation.)
To start the proof, fix any chart xi near m, with xi(m) = 0 for all i, and choose a basis {V(i)} of the tangent space at m such that they satisfy the above condition. With our bare hands, we are now going to specify a new coordinate system be  i =
i =  i(xj) such that
i(xj) such that
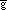 ij =
ij =  V(i), V(j)
V(i), V(j) (showing part (a))
(showing part (a))
The functions  i =
i =  i(xj) will be specified by constructing their inverse xi = xi(
i(xj) will be specified by constructing their inverse xi = xi( j) using a quadratic expression of the form:
j) using a quadratic expression of the form:
| xi | = |  j A(i,j) j A(i,j) | + | 2 |
 j j k B(i,j,k) k B(i,j,k) |
where A(i,j) and B(i,j,k) are constants. It will follow from Taylor's theorem (and the fact that xi (m) = 0 ) that
| A(i,j) | = |  xi xi  j j |
m |
and | B(i,j,k) | = |  2xi 2xi  j j  k k |
m |
so that
| xi | = |  j j |
 xi xi  j j |
m |
+ | 2 |
 j j k k |
 2xi 2xi  j j  k k |
m |
where all the partial derivatives are evaluated at m.
Note These partial derivatives are just (yet to be determined) numbers which, if we differentiate the above quadratic expression, turn out to be its actual partial derivatives evaluated at m.
In order to specify this inverse, all we need to do is specify the terms A(i,j) and B(i,j,k) above.. In order to make the map invertible, we must also guarantee that the Jacobean ( xi/
xi/
 j)m is invertible, and this we shall do.
j)m is invertible, and this we shall do.
We also have the transformation equations
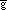 ij ij | = |  xk xk  i i |
 xl xl  j j |
gkl | ... (I) |
and we want these to be specified and equal to  V(i), V(j)
V(i), V(j) when evaluated at m. This is easy enough to do: Just set
when evaluated at m. This is easy enough to do: Just set
| A(i, j) | = |  xi xi  j j |
m |
= | V(j)i. |
For then, no matter how we choose the B(i,j,k) we have
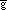 ij(m) ij(m) |
= |
|
|||||||||
| = |
|
||||||||||
| = |
|
as desired. Notice also that, since the {V(i)} are a basis for the tangent space, the change-of-coordinates Jacobean, whose columns are the V(i), is automatically invertible. Also, the V(i) are the coordinate axes of the new system.
 xi/
xi/
 j|m. The number of equations in (I) is not the expected n2, since switching i and j results in the same equation (due to symmetry of the g's). The number of distinct equations is
j|m. The number of equations in (I) is not the expected n2, since switching i and j results in the same equation (due to symmetry of the g's). The number of distinct equations is
| n | + | n 2 |
= | 2 |
, |
leaving us with a total of
| n2 | - | 2 |
of the partial derivatives * In the real world, where n = 4, this is interpreted as saying that we are left with 6 degrees of freedom in choosing local coordinates to be in an inertial frame. Three of these correspond to changing the coordinates by a constant velocity (3 degrees of freedom) or rotating about some axis (3 degrees of freedom: two angles to specify the axis, and a third to specify the rotation).
 xi/
xi/
 j that we can choose arbitrarily. * )
j that we can choose arbitrarily. * )
Next, we want to kill the partial derivatives 
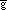 ij/
ij/
 a by choosing appropriate values for the B(i, j, k) (that is, the second order partial derivatives
a by choosing appropriate values for the B(i, j, k) (that is, the second order partial derivatives  2xi/
2xi/
 j
j
 k).By the lemma, it suffices to arrange that
k).By the lemma, it suffices to arrange that
Buthpk(m) = 0.
so it suffices to arrange that
hpk(m)
=
rti(m)
p
xt
xr
h
xi
k
+ p
xt
2xt
h
k
(m) =
p
xt
rti(m)
xr
h
xi
k
+ 
2xt
h
k
(m)
That is, all we need to do is to define
2xt
h
k
(m) = - rti
xr
h
xi
k
(m).
and we are done.
B(t, h, k) = - rti
xr
h
xi
k
(m).
Just close this window to return to the lecture.