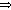Proof

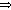(a) (b)

Suppose the coordinate system ⁱ is Lorentz at p, and let xⁱ be as hypothesized in (b). We proceed by invoking condition (a) of Definition 6.2 for several paths. (These paths will correspond to sending out light rays in various directions.)

Path C: x¹ = ct; x² = x³ = 0, x⁴ = t   (a photon traveling along the x¹-axis in E₄).

This gives

T = ( c, 0, 0, 1 ),

and hence ||T||² = 0, and hence Definition 6.2 (a) applies. Let D be the change-of-basis matrix to the (other) inertial frame ⁱ;

Dki

=

i xk

,

so that

i	=	DkiTk
	=	D11 D12 D13 D14 D21 D22 D23 D24 D31 D32 D33 D34 D41 D42 D43 D44 c 0 0 1 .

By property (a) of Definition 6.2,

(¹)² + (¹)² + (¹)² - c²(¹)² = 0,

so that

(cD₁¹ + D¹₄)² + (cD₁² + D²₄)² + (cD₁³ + D³₄)² - c²(cD₁⁴ + D⁴₄)² = 0 ... (*)

If we reverse the direction of the photon, we similarly get

(-cD₁¹ + D¹₄)² + (-cD₁² + D²₄)² + (-cD₁³ + D³₄)² - c²(-cD₁⁴ + D⁴₄)² = 0 ... (**)

Noting that this only effects cross-terms, subtracting and dividing by 4c gives

D₁¹D¹₄ + D₁²D²₄ + D₁³D³₄ - c²D₁⁴D⁴₄ = 0;

that is,

column 1, column 4 = 0 = e₁, e₄ .

In other words, the first and fourth columns of D are orthogonal under the Minkowskian inner product. Similarly, by sending light beams in the other directions, we see that the other columns of D are orthogonal to the fourth column.

If, instead of subtracting, we now add (*) and (**), and divide by 2, we get

c²[D₁¹D₁¹ + D₁² D₁² + D₁³ D₁³ - c²D₁⁴ D₁⁴] + [D₄¹D₄¹ + D₄² D₄² + D₄³ D₄³ - c²D₄⁴ D₄⁴] = 0,

showing that

c² column 1, column 1 = - column 4, column 4 .

So, if we write

column 1, column 1 = k,

then

column 4, column 4 = -c²k       ......     (***)

Similarly (by choosing other photons) we can replace column 1 by either column 2 or column 3, showing that if we take

column 1, column 1 = k,

we have

column i, column i

=

k if 1 i 3 -kc2 if i = 4

.

Let us now take another, more interesting, photon given by

Path D: x¹ = (c/2^1/2)t;   x² = -(c/2^1/2)t;   x³ = 0;   x⁴ = t,   with

T = c/2^1/2, -c/2^1/2, 0, 1 .

(You can check to see that ||T||² = 0, so that it does indeed represent a photon.) Since ||||² = 0, we get

(D₁¹c /2^1/2- D₂¹c /2^1/2+D₄¹)² + (D₁²c /2^1/2- D₂²c /2^1/2+D₄²)² + (D₁³c /2^1/2- D₂³c /2^1/2+D₄³)² - c²(D₁⁴c /2^1/2- D₂⁴c /2^1/2+D₄⁴)²= 0

and, looking at a similar photon traveling in the opposite x²-direction,

(D₁¹c /2^1/2+ D₂¹c/2^1/2+D₄¹)² + (D₁²c/2^1/2+ D₂²c/2^1/2+D₄²)² + (D₁³c/2^1/2+ D₂³c/2^1/2+D₄³)² - c²(D₁⁴c/2^1/2+ D₂⁴c/2^1/2+D₄⁴)²= 0

Subtracting these gives

2c²[D₁¹D₂¹ + D₁² D₂² + D₁³ D₂³ - c²D₁⁴ D₂⁴] + 4c/2^1/2[D₂¹D₄¹ + D₂² D₄² + D₂³ D₄³ - c²D₂⁴ D₄⁴] = 0.

But we already know that the second term vanishes, so we are left with

D₁¹D₂¹ + D₁² D₂² + D₁³ D₂³ - c²D₁⁴ D₂⁴ = 0,

showing that columns 1 and 2 are also orthogonal.

Choosing similar photons now shows us that columns 1, 2, and 3 are mutually orthogonal. Therefore, we have

column i, column j

=

0 if i j k if 1 i = j 3 -kc2 if i = j = 4

.....      (IV)

But, what is k? Let us now invoke condition (b) of Defintion 6.2. To measure the length of a vector in the new frame, we need to transform the metric tensor using this coordinate change. Recall that, using matrix notation, the metric G transforms to = P^TGP, where P is the matrix inverse of D above. In the exercise set, you will see that the columns of P have the same property (IV) above, but with k replaced by 1/k. But,

= P^TGP

Now, since G is just a constant multiple of an elementary matrix, all it does is multiply the last row of P by c². So, when we take P^T(GP), we are really getting the funny dot product of the columns of P back again, which just gives a multiple of G. In other words, we get

= P^TGP = G/k.

Now we invoke condition (b) in Definitoin 6.2: Take the vector = (1, 0, 0, 0) in the -frame. (Recognize it? It is the vector /¹.) Since its 4th coordinate is zero, condition (b) says that its norm-squared must be given by the usual length formula:

||||² = 1.

On the other hand, we can also use to compuate ||||², and we get

||||² =1/k,

showing that k = 1. Hence, = G, and also D has the desired form. This proves (b) (and also (c), by the way).

(b) 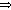(c)

If the change of coordinate matrix has the above orthogonality property,

Di1Dj1 + Di2 Dj2 + Di3 Dj3 - c2Di4 Dj4

=

column i, column j

=

0 if i j 1 if 1 i = j 3 -c2 if i = j = 4

,

then the argument in (a) 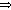(b) shows that = G (since k = 1/k = 1 here).

(c) (a)

If = diag[1, 1, 1, -c²] at the point p, then is Lorentz at p, by the remarks preceding Definition 6.2. Thus, we are done.

Just close this window to return to the lecture.