We now generalize the ideas discussed in Lecture 1.

Definition 2.1 An open cover of M Es is a collection {Ua} of open sets in M such that M = aUa.

Examples

(a) E_s can be covered by open balls.

(b) E_s can be covered by the single (open) set E_s.

(c) The unit sphere in E_s can be covered by the collection {U₁, U₂} where

U₁ = {(y₁, y₂, y₃) | y₃ > -1/2}
U₂ = {(y₁, y₂, y₃) | y₃ < 1/2}.

Definition 2.2 A subset M of Es is called an n-dimensional smooth manifold if we are given a collection {Ua; xa1, xa2, . . ., xan} where: (a) The Ua form an open cover of M. (b) Each xar is a smooth (what does that mean?) real-valued function defined on U (that is, xar: UaE1), called the th coordinate, such that the map x: UaEn given by x(u) = (xa1(u), xa2(u), . . . , xan(u)) is one-to-one. (That is, to each point in Ua, we are assigned a unique set of n coordinates.) The tuple (Ua; xa1, xa2, . . ., xan) is called a local chart of M. The collection of all charts is called a smooth atlas of M. Further, Ua is called a coordinate neighborhood. (c) If (U, xi), and (V, j) are two local charts of M, and if UV , then we can write xi = xi(j) with inverse k = k(xl) for each i and k, where all functions in sight are smooth. These functions are called the change-of-coordinates transformations.

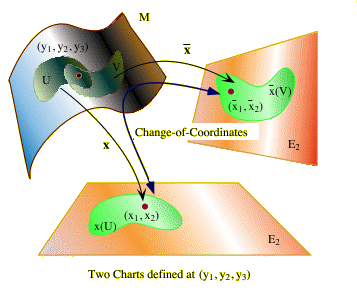By the way, we call the "big" space E_s in which the manifold M is embedded the ambient space.

Notes
1. Always think of the xⁱ as the local coordinates (or parameters) of the manifold. We can paramaterize each of the open sets U by using the inverse function x^-1 of x, which assigns to each point in some neighborhood of E_n a corresponding point in the manifold. Let me see an example.
2. Condition (c) implies that

det

i xj

0,

and




det

xi j

0

,

since the associated matrices must be invertible.
3. The ambient space need not be present in the general theory of manifolds; that is, it is possible to define a smooth manifold M without any reference to an ambient space at all -- see any text on differential topology or differential geometry.
4. More terminology: We shall sometimes refer to the xⁱ as the local coordinates, and to the y^j as the ambient coordinates. Thus, a point in an n-dimensional manifold M in E_s has n local coordinates, but s ambient coordinates.

Examples 2.3
(a) E_n is an n-dimensional manifold, with the single identity chart defined by

xⁱ(y₁, . . . , y_n) = y_i.

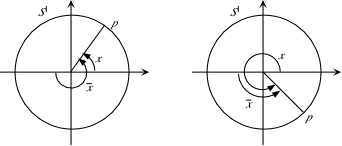
One has

x: S¹-{(1, 0)} E₁ : S¹-{(-1, 0)} E₁,

=

+x if x < -x if x >   (See the figure for the two cases.)

x

=

+ if < - if > ,

Notice the symmetry between x and . Also notice that these change-of-coordinate functions are only defined when 0, . Further,

/x = x/ = 1.

Note that, in terms of complex numbers, we can write, for a point p = e^iz S¹,

x = arg(z), = arg(-z).

(c) Generalized Polar Coordinates Let us take M = Sⁿ, the unit n-sphere,

Sⁿ = {(y₁, y₂, ... , y_n, y_n+1) E_n+1 | _iy_i² = 1},

with coordinates (x¹, x², . . . , xⁿ) with

0 < x¹, x², . . . , x^n-1 < ,   and
0 < xⁿ < 2,

y₁ = cos x¹
y₂ = sin x¹ cos x²
y₃ = sin x¹ sin x² cos x³
...
y_n-1 = sin x¹ sin x² sin x³ sin x⁴ ... cos x^n-1
y_n = sin x¹ sin x² sin x³ sin x⁴ ... sin x^n-1 cos xⁿ
y_n+1 = sin x¹ sin x² sin x³ sin x⁴ ... sin x^n-1 sin xⁿ

In the homework, you will be asked to obtain the associated chart by solving for the xⁱ. Note that if the sphere has radius r, then we can multiply all the above expressions by r, getting

y₁ = r cos x¹
y₂ = r sin x¹ cos x²
y₃ = r sin x¹ sin x² cos x³
...
y_n-1 = r sin x¹ sin x² sin x³ sin x⁴ ... cos x^n-1
y_n = r sin x¹ sin x² sin x³ sin x⁴ ... sin x^n-1 cos xⁿ
y_n+1 = r sin x¹ sin x² sin x³ sin x⁴ ... sin x^n-1 sin xⁿ.

(d) The torus T = S¹S¹, with the following four charts:

x: (S¹-{(1, 0)})(S¹-{(1, 0)})E₂, given by
x¹((cos, sin), (cos, sin)) =
x²((cos, sin), (cos, sin)) = .

(e) The cylinder (exercise)

(f) Sⁿ, with (again) stereographic projection, is an n-manifold; the two charts are given as follows. Let P be the point (0, 0, . . , 0, 1) and let Q be the point (0, 0, . . . , 0, -1). Then define two charts (Sⁿ-P, xⁱ) and (Sⁿ-Q, ⁱ) as follows. (See the figure.)

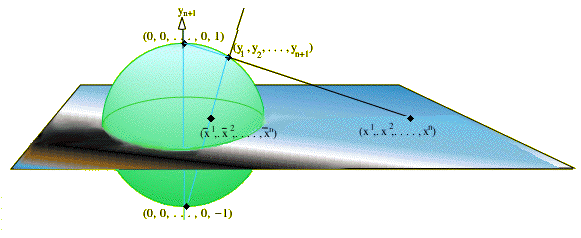
If (y₁, y₂, . . . , y_n, y_n+1) is a point in Sⁿ, let

x1 = y1 1 - yn+1		1 = y1 1 + yn+1
x2 = y2 1 - yn+1		2 = y2 1 + yn+1
. . .		. . .
xn = yn 1 - yn+1		n = yn 1 + yn+1

We can invert these maps (that is, solve for the global coordinates y_i in terms of the local coordinates x_i and _i) as follows:

Let r² = _i xⁱxⁱ, and ² = _i ⁱⁱ. Then:

y1 = 2x1 r2 + 1		y1 = 21 1+2
y2 = 2x2 r2 + 1		y2 = 22 1+2
. . .		. . .
yn = 2xn r2 + 1		yn = 2n 1+2
yn+1 = r2 - 1 r2 + 1		yn+1 = 1 - 2 1+2

The change-of-coordinate maps are therefore:

x1	=	y1 1 - yn+1	=	21 1+2 1 - 1 - 2 1 + 2	=	1 2
x2					=	2 2
. . .
xn					=	n 2

This makes sense, since the maps are not defined when ⁱ = 0 for all i, corresponding to the north pole.

Note Since is the distance from ⁱ to the origin, this map is hyperbolic reflection in the unit circle;

xi = 1

i

and squaring and adding gives

r = 1/

That is, project it to the circle, and invert the distance from the origin. This also gives the inverse relations, since we can write

ⁱ = ²xⁱ = xⁱ/r².

In other words, we have the following transformation rules.

Note We can put all the coordinate functions x_a^r: U_aE₁ together to get a single map

x_a: U_aW_a E_n.

A more precise formulation of condition (c) in the definition of a manifold is then the following: each W_a is an open subset of E_n, each x_a is invertible, and each composite

Wa

xa-1

En

xb

Wb

is a smooth function defined on an open subset.

We now want to discuss scalar and vector fields on manifolds, but how do we specify such things? First, a scalar field.

Definition 2.4 A smooth scalar field on a smooth manifold M is just a smooth real-valued map : ME1. (In other words, it is a smooth function of the coordinates of M as a subset of Er.) Thus, associates to each point m of M a unique scalar (m). If U is a subset of M, then a smooth scalar field on U is smooth real-valued map : UE1. If U M, we sometimes call such a scalar field local.

If is a scalar field on M and x is a chart, then we can express as a smooth function of the associated parameters x¹, x², . . . , xⁿ. If the chart is , we shall write for the function of the other parameters ¹, ², . . . , ⁿ. Note that we must have = at each point of the manifold (see the transformation rule below).

Examples 2.5 (a) Let M = E_n (with its usual structure) and let be any smooth real-valued function in the usual sense. Then, using the identity chart, we have = .

(b) Let M = S², and define (y₁, y₂, y₃) = y₃.
Using stereographic projection, we find both and :

(x1, x2)	=	y3(x1, x2)	=	r2 - 1 r2 + 1	=	(x1)2 + (x2)2 - 1 (x1)2 + (x2)2 + 1
(1, 2)	=	y3(1, 2)	=	1 - 2 1 + 2	=	1 - (1)2 - (2)2 1 + (1)2 + (2)2

(c) Local Scalar Field The most obvious candidate for local fields are the coordinate functions themselves. If U is a coordinate neighborhood, and x = {xⁱ} is a chart on U, then the maps xⁱ are local scalar fields.

Sometimes, as in the above example, we may wish to specify a scalar field purely by specifying it in terms of its local parameters; that is, by specifying the various functions instead of the single function . The problem is, we can't just specify it any way we want, since it must give a value to each point in the manifold independently of local coordinates. That is, if a point p M has local coordinates (x^j) with one chart and (^h) with another, they must be related via the relationship

^j = ^j(x^h).

Example 2.6 Look at Example 2.5(b) above. If you substituted ⁱ as a function of the x^j, you would get (¹, ²) = (x¹, x²) (after some laborious albegra!).

1. Give the paraboloid z = x² + y² the structure of a smooth manifold.

2. Find a smooth atlas of E₂ consisting of three charts.

3. (a) Extend the method in Exercise 1 to show that the graph of any smooth function f: E₂E₁ can be given the structure of a smooth manifold.
(b) Generalize part (a) to the graph of a smooth function f: E_n E₁.

4. Two atlases of the manifold M give the same smooth structure if their union is again a smooth atlas of M.
(a) Show that the smooth atlases (E₁, f), and (E₁, g), where f(x) = x and g(x) = x³ are incompatible.
(b) Find a third smooth atlas of E₁ that is incompatible with both the atlases in part (a).

5. Consider the ellipsoid L E₃ specified by

x2 a2 + y2 b2 + z2 c2

=

1,

(a, b, c 0). Define f: LS² by f(x, y, z) = (x/a, y/b. z/c).
(a) Verify that f is invertible (by finding its inverse).
(b) Use the map f, together with a smooth atlas of S², to construct a smooth atlas of L.

6. Find the chart associated with the generalized spherical polar coordinates described in Example 2.3(c) by inverting the coordinates. How many additional charts are needed to get an atlas? Give an example.

7. Obtain the equations in Example 2.3(f).