 i i  j j |
= |  i i |
Vk |  j j |
Wm | = |  i i |
 j j |
Vk Wm | , |
| Table of Contents | Back to Lecture 4: Contravariant and Covariant Vector Fields | On to Lecture 6: Riemannian Manifolds |
Lecture 4 described vector fields on manifolds. We now look at tensors on smooth manifolds.
Suppose that v = (v1, v2, v3) and w = (w1, w2, w3) are vector fields on E3. Then their tensor product is defined to consist of the nine quantities viwj.
Let us see how such things transform. Thus, let V and W be contravariant, and let C and D be covariant. Then:
 i i  j j |
= |  i i |
Vk |  j j |
Wm | = |  i i |
 j j |
Vk Wm | , |
and similarly,
 i i  j j |
= |  i i |
 j j |
Vk Cm | , |
and
 i i  j j |
= |  j j |
 j j |
Ck Dm | . |
We call these product fields "tensors" of type (2, 0), (1, 1), and (0, 2) respectively.
| Definition 5.1 A tensor field of type (2, 0) on the n-dimensional smooth manifold M associates with each chart x a collection of n2 smooth functions Tij(x1, x2, . . . , xn) which satisfy the transformation rules shown below. Similarly, we define tensor fields of type (0, 2), (1, 1), and, more generally, a tensor field of type (m, n). |
Some Tensor Transformation Rules
|
Note A tensor field of type (1, 0) is just a contravariant vector field, while a tensor field of type (0, 1) is a covariant vector field. Similarly, a tensor field of type (0, 0) is a scalar field. Type (1, 1) tensors correspond to linear transformations in linear algebra.
Examples 5.2
(a) Of course, by definition, we can take tensor products of vector fields to obtain tensor fields, as we did above in Definition 4.1.
(b) The Kronecker Delta Tensor, given by
 ji ji | = |
|
is, in fact a tensor field of type (1, 1). Indeed, one has
 ji ji | = | , |
and the latter quantities transform according to the rule
 | i j |
= |  i i |
 j j |
|
| = |  i i |
 j j |
 km km |
whence they constitute a tensor field of type (1, 1).
Question OK, so is this how it works: Given a point p of the manifold and a chart x at p this strange object assigns the n2< quantities  ij; that is, the identity matrix, regardless of the chart we chose?
ij; that is, the identity matrix, regardless of the chart we chose?
Answer Yes.
Question But how can we interpret this strange object?
Answer Just as a covariant vector field converts contravariant fields into scalars (see Lecture 3) we shall see that a type (1,1) tensor converts contravariant fields to other contravariant fields. This particular tensor does nothing: put in a specific vector field V, out comes the same vector field. In other words, it is the identity transformation.
Notes
| 1. |  ij is independent of the chart used (the coordinates are the same as the barrd coordinates). Also, ij is independent of the chart used (the coordinates are the same as the barrd coordinates). Also,  ij = ij =  ji. That is, it is a symmetric tensor. ji. That is, it is a symmetric tensor. |
||||||
| 2. |
|
(c) We can make new tensor fields out of old ones by taking products of existing tensor fields in various ways. For example,
while
Specific examples of these involve the Kronecker delta, and are in the homework.
(d) If X is a contravariant vector field, then the functions Xi/
xjdo not define a tensor.
Indeed, let us check the transformation rule directly:
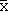 i i j j | = |
|
|||||||
| = |
|
||||||||
| = |
|
We will see more interesting examples later.
|
Proposition 5.3 (If It Looks Like a Tensor, It Is a Tensor)
Suppose that we are given smooth local functions gij with the property that for every pair of contravariant vector fields Xi and Yi, the smooth functions gijXiYj determine a scalar field. Then the gij determine a smooth tensor field of type (0, 2). |
Proof Since the gijXiYj form a scalar field, we must have
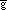 ij
ij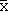 i
i j = ghkXhYk.
j = ghkXhYk.On the other hand,
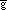 ij ij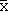 i i j j |
= | 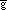 ijXhYk ijXhYk |
 i i |
 j j |
by the transformation rules for contravariant vectors. Equating the right-hand sides gives
| ghkXhYk | = | 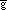 ij ij |
 i i |
 j j |
XhYk | ..................... | (I) |
Now, if we could only cancel the terms XhYk! Well, choose a point m  M. It suffices to show that
M. It suffices to show that
| ghk | = | 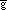 ij ij |
 i i |
 j j |
, |
when evaluated at the coordinates of m. However, by Example 4.3(c), we can arrange for vector fields X and Y such that
| Xi(coordinates of m) | = |
|
, |
and
| Yi(coordinates of m) | = |
|
. |
Substituting these into equation (I) now gives the required transformation rule.
Example 5.4 Metric Tensor

Define a set of quantities gij by
| gij | = | . |
Question Why should I believe that this is a tensor?
Answer Let us invoke the above proposition: If Xi and Yj are any contravariant fields on M, then their dot product X.Y is a scalar, and
| X . Y | = | Xi | . | Yj | = | gijXiYj | . |
Thus, by Proposition 5.3, it is a type (0, 2) tensor. We call this tensor "the metric tensor inherited from the imbedding of M in Es."
Exercise Set 5
1. Compute the transformation rules for each of the following, and hence decide whether or not they are tensors. Sub-and superscripted quantities (other than coordinates) are understood to be tensors.
| (a) | dt |
(b) | (c) | (d) |  |
(e) |
2. (Rund, p. 95 #3.4) Show that if Aj is a type (0, 1) tensor, then
| - |
is a type (0, 2) tensor.
3. Show that, if M and N are tensors of type (1, 1), then:
4. Let X be a contravariant vector field, and suppose that M is such that all change-of-coordinate maps have the form  i = aijxj + ki for certain constants aij and kj. (We call such a manifold affine.) Show that the functions
i = aijxj + ki for certain constants aij and kj. (We call such a manifold affine.) Show that the functions Xi/
xj define a tensor field of type (1, 1).
5. (Rund, p. 96, 3.12) If Bijk = -Bjki, show that Bijk = 0. Deduce that any type (3, 0) tensor that is symmetric on the first pair of indices and skew-symmetric on the last pair of indices vanishes.
6. (Rund, p. 96, 3.16) If Akj is a skew-symmetric tensor of type (0, 2), show that the quantities Brst defined by
| Brst | = | + | + |
(a) are the components of a tensor; and
(b) are skew-symmetric in all pairs in indices.
(c) How many independent components does Brst have?
8. Suppose that Cij is a type (2, 0) tensor, and that, regarded as an nŔn matrix C, it happens to be invertible in every coordinate system. Define a new collection of functions, Dij by taking
the ij the entry of C-1 in every coordinate system. Show that Dij, is a type (0, 2) tensor. [Hint: Write down the transformation equation for Cij and invert everything in sight.]
| Table of Contents | Back to Lecture 4: Contravariant and Covariant Vector Fields | On to Lecture 6: Riemannian Manifolds |