Lecture 7: Locally Minkowskian Manifolds: A Little Relativity
In the last lecture, we saw how we can use a Riemannian metric to measure distance. Here, we look at a very special metric.
First a general comment: We said in the last section that, at any point p in a Riemannian manifold M, we can find a local chart at p with the property that the metric tensor g** is diagonal, with diagonal terms  1. In particular, we said that Minkowski space comes with a such a metric tensor having signature (1, 1, 1, -1). Now there is nothing special about the number 1 in the discussion: we can also find a local chart at any point p with the property that the metric tensor g** is diagonal, with diagonal terms any non-zero numbers we like (although we cannot choose the signs).
1. In particular, we said that Minkowski space comes with a such a metric tensor having signature (1, 1, 1, -1). Now there is nothing special about the number 1 in the discussion: we can also find a local chart at any point p with the property that the metric tensor g** is diagonal, with diagonal terms any non-zero numbers we like (although we cannot choose the signs).
In relativity, we take deal with 4-dimensional manifolds, and take the first three coordinates x1, x2, x3 to be spatial (measuring distance), and the fourth one, x4, to be temporal (measuring time). Let us postulate that we are living in some kind of 4-dimensional manifold M (since we want to include time as a coordinate. By the way, we refer to a chart x at the point p as a frame of reference, or just frame). Suppose now we have a particle -- perhaps moving, perhaps not -- in M. Assuming it persists for a period of time, we can give it spatial coordinates (x1, x2, x3) at every instant of time (x4). Since the first three coordinates are then functions of the fourth, it follows that the particle determines a path in M given by
x1 = x1(x4)
x2 = x2(x4)
x3 = x3(x4)
x4 = x4,
so that x4 is the parameter. This path is called the world line of the particle. Mathematically, there is no need to use x4 as the parameter, and so we can describe the world line as a path of the form
where t is some parameter. (Note: t is not time; it's just a parameter. x4 is time). Conversely, if t is any parameter, and xi = xi(t) is a path in M, then, if x4 is an invertible function of t, that is, dx4/dt 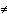 0 (so that, at each time x4, we can solve for the other coordinates uniquely) then we can solve for x1, x2, x3 as smooth functions of x4, and hence picture the situation as a particle moving through space.
0 (so that, at each time x4, we can solve for the other coordinates uniquely) then we can solve for x1, x2, x3 as smooth functions of x4, and hence picture the situation as a particle moving through space.
Now, let's assume our particle is moving through M with world line xi = xi(t) as seen in our frame (local coordinate system). The velocity and speed of this particle (as measured in our frame) are given by
| v |
= |
 |
dx1

dx4 |
, |
dx2

dx4 |
, |
dx3

dx4 |
 |
| speed2 |
= |
 |
dx1

dx4 |
 |
2
|
+ |
 |
dx2

dx4 |
 |
2
|
+ |
 |
dx3

dx4 |
 |
2
|
. |
The problem is, we cannot expect v to be a vector -- that is, satisfy the correct transformation laws. But we do have a contravariant 4-vector
| Ti |
= |
dxi

dt |
(T stands for tangent vector. Also, remember that t is not time). If the particle is moving at the speed of light c, then
 |
dx1

dx4 |
 |
2
|
+ |
 |
dx2

dx4 |
 |
2
|
+ |
 |
dx3

dx4 |
 |
2
|
= |
c2 | ...... (I) |
| |
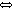 |
 |
dx1

dt |
 |
2
|
+ |
 |
dx2

dt |
 |
2
|
+ |
 |
dx3

dt |
 |
2
|
= |
c2 |
 |
dx4

dt |
 |
2
|
(using the chain rule) |
| |
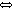 |
 |
dx1

dt |
 |
2
|
+ |
 |
dx2

dt |
 |
2
|
+ |
 |
dx3

dt |
 |
2
|
- |
c2 |
 |
dx4

dt |
 |
2
|
= |
0. |
Now this looks like the norm-squared, ||T||2, of the vector T under the metric whose matrix is
| g** | = |
diag[1, 1, 1, -c2] |
= |
 | |  | . |
|
In other words, the particle is moving at light-speed 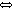 ||T||2 = 0
||T||2 = 0 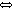 ||T|| is null
under this rather interesting local metric. So, to check whether a particle is moving at light speed, just check whether T is null.
||T|| is null
under this rather interesting local metric. So, to check whether a particle is moving at light speed, just check whether T is null.
Question What's the -c2 doing in place of -1 in the metric?
Answer Since physical units of time are (usually) not the same as physical units of space, we would like to convert the units of x4 (the units of time) to match the units of the other axes. Now, to convert units of time to units of distance, we need to multiply by something with units of distance/time; that is, by a non-zero speed. Since relativity holds that the speed of light c is a universal constant, it seems logical to use c as this conversion factor.
Now, if we happen to be living in a Riemannian 4-manifold whose metric diagonalizes to something with signature (1, 1, 1, -c2), then the physical property of traveling at the speed of light is measured by ||T||2, which is a scalar, and thus independent of the frame of reference. In other words, we have discovered a metric signature that is consistent with the requirement that the speed of light is constant in all frames in which g** has the above diagoal form (so that ita makes sense to say what the speed if light is.)
|
Definition 7.1 A Riemannian 4-manifold M is called locally Minkowskian if its metric has signature (1, 1, 1, -c2).
|
For the rest of this section, we will be in a locally Minkowskian manifold M.
Note If we now choose a chart x in locally Minkowskian space where the metric has the diagonal form diag[1, 1, 1, -c2] shown above at a given point p, then we have, at the point p:
(a) If any path C has ||T||2 = 0, then
 |
dx1

dt |
 |
2
|
+ |
 |
dx2

dt |
 |
2
|
+ |
 |
dx3

dt |
 |
2
|
- |
c2 |
 |
dx4

dt |
 |
2
|
= |
0 |
(because this is how we calculate ||T||2)
(b) If V is any contravariant vector with zero x4-coordinate, then
||V||2 = (V1)2 + (V2)2 + (V3)2 (for the same reason as above)
(a) says that we measure the world line C as representing a particle traveling with light speed, and (b) says that we measure ordinary length in the usual way. This motivates the following definition.
It follows from the remark preceding the defintion that if x is any chart such that, at the point p, the metric has the nice form diag[1, 1, 1, -c2], then x is a Lorentz frame at the point p. Note that in general, the coordinates of T in the system  i are given by matrix multiplication with some possibly complicated change-of-coordinates matrix, and to further complicate things, the metric may look messy in the new coordinate system. Thus, very few frames are going to be Lorentz.
i are given by matrix multiplication with some possibly complicated change-of-coordinates matrix, and to further complicate things, the metric may look messy in the new coordinate system. Thus, very few frames are going to be Lorentz.
|
Physical Interpretation of a Lorentz Frame
What the definition means physically is that an observer in the  -frame who measures a particle traveling at light speed in the x-frame will also reach the conclusion that its speed is c, because he makes the decision based on (I), which is equivalent to (II). In other words: -frame who measures a particle traveling at light speed in the x-frame will also reach the conclusion that its speed is c, because he makes the decision based on (I), which is equivalent to (II). In other words:
A Lorentz frame in locally Minkowskian space is any frame in which light appears to be traveling at light speed, and where we measure length in the usual way.
|
Question Do all Lorentz frames at p have the property that metric has the nice form diag[1, 1, 1, -c2]?
Answer Yes, as we shall see below.
Question OK. But if x and  are two Lorentz frames at the point p, how are they related?
are two Lorentz frames at the point p, how are they related?
Answer Here is an answer. First, continue to denote a specific Lorentz frame at the point p by x.
|
Theorem 7.3 (Criterion for Lorentz Frames)
The following are equivalent for a locally Minkowskian manfifold M:
(a) A coordinate system  i in Minkowski space M is Lorentz at the point p i in Minkowski space M is Lorentz at the point p
(b) If x is any frame such that, at p, G = diag[1, 1, 1, -c2], then the columns of the change-of-coordinate matrix
satisfy
 column i, column j column i, column j  = =  ei, ej ei, ej  , ,
where the inner product is defined by the matrix G.
(c)  = diag[1, 1, 1, -c2] = diag[1, 1, 1, -c2]
|
Click here for a proof.
We will call the transformation from one Lorentz frame to another a generalized Lorentz transformation.
An Example of a Lorentz Transformation
We would like to give a simple example of such a transformation matrix D, so we look for a matrix D whose first column has the general form  a, 0, 0, b
a, 0, 0, b  , with a and b non-zero constants. (Why? If we take b = 0, we will wind up with a less interesting transformation: a rotation in 3-space.) There is no loss of generality in taking a = 1, so let us use
, with a and b non-zero constants. (Why? If we take b = 0, we will wind up with a less interesting transformation: a rotation in 3-space.) There is no loss of generality in taking a = 1, so let us use  1, 0, 0, -
1, 0, 0, - /c
/c  . Here, c is the speed of light, and
. Here, c is the speed of light, and  is a certain constant. (The meaning of
is a certain constant. (The meaning of  will emerge in due course). Its norm-squared is (1 -
will emerge in due course). Its norm-squared is (1 -  2), and we want this to be 1, so we replace the vector by
2), and we want this to be 1, so we replace the vector by
| ( |
1

(1 -  2)1/2 2)1/2 |
, |
0 |
, |
0 |
, |
- /c /c

(1 -  2)1/2 2)1/2 |
) |
. |
This is the first column of D. To keep things simple, let us take the next two columns to be the corresponding basis vectors e2, e3. Now we might be tempted to take the forth vector to be e4, but that would not be orthogonal to the above first vector. By symmetry (to get a zero inner product) we are forced to take the last vector to be
| ( |
- c c

(1 -  2)1/2 2)1/2 |
, |
0 |
, |
0 |
, |
1

(1 -  2)1/2 2)1/2 |
) |
. |
This gives the transformation matrix as
| D |
= |
 |
1

(1 -  2)1/2 2)1/2 |
0 | 0 |
- c c

(1 -  2)1/2 2)1/2 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
- /c /c

(1 -  2)1/2 2)1/2 |
0 | 0 |
1

(1 -  2)1/2 2)1/2 |
|
 |
, |
and hence the new coordinates (by integrating everything in sight; using the boundary conditions  i = 0 when xi = 0) as
i = 0 when xi = 0) as
 1 1 | = |
x1 -  cx4 cx4

(1 -  2)1/2 2)1/2 |
; |
 2 = x2 2 = x2 |
; |
 3 = x3 3 = x3 |
; |
 4 4 | = |
x4 -  x1/c x1/c

(1 -  2)1/2 2)1/2 |
; |
Notice that solving the first equation for x1 gives
Since x4 is just time t here, it means that the origin of the  -system has coordinates (
-system has coordinates ( ct, 0, 0) in terms of the original coordinates. In other words, it is moving in the x-direction with a velocity of
ct, 0, 0) in terms of the original coordinates. In other words, it is moving in the x-direction with a velocity of
v =  c,
c,
so we must interpret  as the speed in "warp;"
as the speed in "warp;"
 = v/c.
= v/c.
This gives us the famous
Exercise Set 7
1. What can be said about the scalar ||dxi/dt||2 in a Lorentz frame for a particle traveling at (a) sub-light speed (b) super-light speed?
2. (a) Show that, if xi(t) is a timelike path in the Minkowskian manifold M so that dx4/dt 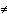 0, then d
0, then d 4/dt
4/dt 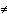 0 in every Lorentz frame
0 in every Lorentz frame  . In other words, if a particle is moving at sub-light speed in any one Lorentz frame, then it is moving at sub-light speed in all Lorentz frames.
. In other words, if a particle is moving at sub-light speed in any one Lorentz frame, then it is moving at sub-light speed in all Lorentz frames.
(b) Conclude that, if a particle is traveling at super-light speed in one Lorentz frame, then it is traveling at super-light speeds in all such frames.
3. Referring to the Lorentz transformations for special relativity, consider a "photon clock" constructed by bouncing a single photon back and forth bewtwwen two parallel mirrors as shown in in the following figure.
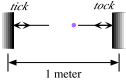
Now place this clock in a train moving in the x-direction with velocity v. By comparing the time it takes between a tick and a tock for a stationary observer and one on the train, obtain the time contraction formula (
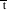 in terms
in terms  t) from the length contraction one.
t) from the length contraction one.
4. Prove the claim in the proof of 7.3, that if D is a 4 4 matrix whose columns satisfy
4 matrix whose columns satisfy
 column i, column j column i, column j  |
= |
 |
| 0 | if | i 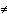 j j |
| k | if | 1  i = j i = j  3 3 |
| -kc2 | if | i = j = 4 | |
, |
using the Minkowski inner product G (not the standard inner product), then D-1 has its columns satisfying
 column i, column j column i, column j  |
= |
 |
| 0 | if | i 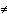 j j |
| 1/k | if | 1  i = j i = j  3 3 |
| -c2/k | if | i = j = 4 | |
. |
[Hint: use the given property of D to write down the entries of its inverse P in terms of the entries of D.]
5. Invariance of the Minkowski Form
Show that, if P = xi0 and Q = xi0 +  xi are any two events in the Lorentz frame xi, then, for all Lorenz frames
xi are any two events in the Lorentz frame xi, then, for all Lorenz frames  i, one has
i, one has
( x1)2 + (
x1)2 + ( x2)2+ (
x2)2+ ( x3)2- c2(
x3)2- c2( x4)2 = (
x4)2 = (
 1)2 + (
1)2 + (
 2)2+ (
2)2+ (
 3)2- c2(
3)2- c2(
 4)2
4)2
[Hint: Consider the path xi(t) = x0i +  xit, so that dxi/dt is independent of t. Now use the transformation formula to conclude that d
xit, so that dxi/dt is independent of t. Now use the transformation formula to conclude that d i/dt is also independent of t. (You might have to transpose a matrix before multiplyingÉ) Deduce that
i/dt is also independent of t. (You might have to transpose a matrix before multiplyingÉ) Deduce that  i(t) = zi + rit for some constants ri and si. Finally, set t = 0 and t = 1 to conclude that
i(t) = zi + rit for some constants ri and si. Finally, set t = 0 and t = 1 to conclude that  i(t) =
i(t) =  0i +
0i + 
 it, and apply (c) above.]
it, and apply (c) above.]
6. If the  i-system is moving with a velocity v in a certain direction with resepct to the xi-system, we call this a boost in the given direction. Show that successive boosts in two perpendicular directions do not give a "pure" boost (the spatial axes are rotated-no longer parallel to the original axes). Now do some reading to find the transformation for a pure boost in an arbitrary direction.
i-system is moving with a velocity v in a certain direction with resepct to the xi-system, we call this a boost in the given direction. Show that successive boosts in two perpendicular directions do not give a "pure" boost (the spatial axes are rotated-no longer parallel to the original axes). Now do some reading to find the transformation for a pure boost in an arbitrary direction.
Last Updated: January, 2002
Copyright © Stefan Waner
 1. In particular, we said that Minkowski space comes with a such a metric tensor having signature (1, 1, 1, -1). Now there is nothing special about the number 1 in the discussion: we can also find a local chart at any point p with the property that the metric tensor g** is diagonal, with diagonal terms any non-zero numbers we like (although we cannot choose the signs).
1. In particular, we said that Minkowski space comes with a such a metric tensor having signature (1, 1, 1, -1). Now there is nothing special about the number 1 in the discussion: we can also find a local chart at any point p with the property that the metric tensor g** is diagonal, with diagonal terms any non-zero numbers we like (although we cannot choose the signs).
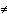 0 (so that, at each time x4, we can solve for the other coordinates uniquely) then we can solve for x1, x2, x3 as smooth functions of x4, and hence picture the situation as a particle moving through space.
0 (so that, at each time x4, we can solve for the other coordinates uniquely) then we can solve for x1, x2, x3 as smooth functions of x4, and hence picture the situation as a particle moving through space.
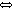
 M is any coordinate system
M is any coordinate system  i with the following properties:
(a) If any path C has the scalar ||T||2 = 0, then, at p,
i with the following properties:
(a) If any path C has the scalar ||T||2 = 0, then, at p,

 ,
,  is not of this form, since
is not of this form, since 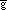 ij may not be be diagonal)
ij may not be be diagonal)
 1)2 + (
1)2 + (
 = diag[1, 1, 1, -c2]
= diag[1, 1, 1, -c2]
 /c
/c 

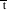 in terms
in terms  4 matrix whose columns satisfy
4 matrix whose columns satisfy
 i = j
i = j