Continuity & Differentiability
|
Return to Main Page
Part A: Continuity Exercises for This Topic Index of On-Line Topics Everything for Calculus Everything for Finite Math Everything for Finite Math & Calculus Utility: Function Evaluator & Grapher Español |
Part B: Differentiability
Note To understand this topic, you will need to be familiar with limits, as discussed in the chapter on derivatives in Calculus Applied to the Real World. If you like, you can review the topic summary material on derivatives and limits or, for a more detailed study, the on-line tutorial on derivatives.
To begin, we recall the definition of the derivative of a function, and what it means for a function to be differentiable.
|
Derivative; Differentiability
The derivative of the function $f$ at the point $a$ in its domain is given by
The function $f$ is differentiable on the subset $S$ of its domain if it differentiable at each point of $S.$ Note
 |
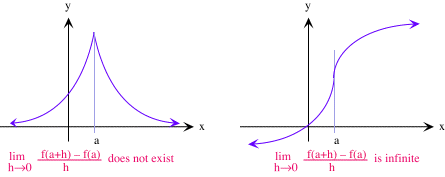Example 1 Functions Not Differentiable at Isolated Points
Determine points of non-differentiability of the following functions
Solution
(a)
The power rule tells us that $f(x) = (x-1)^{1/3}$ has derivative $f'(x) = (1/3)(x-1)^{-2/3}$ everywhere where this expression is defined, and is not diffeentiable when $(1/3)(x-1)^{-2/3}$ is not defined. Since $(x-1)$ has a negative exponent, $f'(x)$ is not defined when $x = 1,$ and so $f$ is not differentible there. In fact, direct calculation shows that
| $lim$ $h→0$ |
$\frac{f(1+h) - f(1)}{h} =$ | $lim$ $h→0$ |
$\frac{h^{1/3}}{h} =$ | $lim$ $h→0$ |
$\frac{1}{h^{2/3}} = +∞,$ |
| (b) | Since $g(x) = \|x+2\| =$ |  | $-(x+2)$ $x+2$ | if $x ≤ -2$ if $x > -2$ |
, |
| $lim$ $h→0$ |
$\frac{f(-2+h) - f(-2)}{h} =$ | $lim$ $h→0$ |
(c) The quotient rule tells us that $r(x) = x^2/(x - 1)$ is differentiable everywhere except at $x = 1.$ However, $x = 1$ is not in the domain of $r,$ and so $r$ is differentiable at every point of its domain.
As we see in the graph on the right, there are no points of vertical tangency or cusps.
Before We Go On...
As you can see, the graphs provide immediate information as to where to look for a point of non-differentiability: a point where there appears to be a cusp or a vertical tangent.
Here is one for you.
Example 2 Points of Non-Dfferentiability
Q In Part A we discussed continuity, and here we discussed differentiability. Are all continuous functions differentiable? Are all differentiable functions continuous?
Theorem Differentiability Implies Continuity
| $lim$ $h→0$ |
exists, and equals $f'(a).$ |
| $lim$ $h→0$ |
$f(a+h) - f(a) =$ | $lim$ $h→0$ |
$\frac{f(a+h) - f(a)}{h} ^{.} h = f'(a) ^{.} 0 = 0.$ | Limit of product $=$ product of limits |
| $lim$ $h→0$ |
$f(a+h) =$ | $lim$ $h→0$ |
$[f(a+h) - f(a)] + f(a) = 0 + f(a) = f(a).$ | Limit of sum $=$ sum of limits |
| $lim$ $x-a→0$ |
$f(x) = f(a).$ |
| $lim$ $x→a$ |
$f(x) = f(a),$ |
You can now either go on and try the rest of the exericses in the exercise set for this topic.