The Trigonometric Functions
by
Stefan Waner and Steven R. Costenoble

This Section: 1. Modeling with the Sine Function

Section 1 Exercises

2. The Six Trigonometric Functions

Trigonometric Functions Main Page

"RealWorld" Page

Everything for Calculus

Español

1. Modeling with the Sine Function

Take a look at the following graph, which shows the approximate average daily high temperature in New York's Central Park. ^#

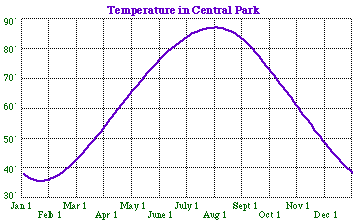
^#Source: National Weather Service/The New York Times, January 7, 1996, p. 36.

Each year, the pattern repeats over and over, resulting in the following graph.

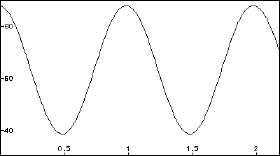Here, the $x-$coordinate represents time in years with $x = 0$ representing August 1, while the $y-$coordinate represents the termperature in $ ^oF.$ This is an example of cyclical or periodic behavior.

Cyclical behavior is common in the business world; just as there are seasonal fluctuations in the temperature in Central Park, there are seasonal fluctuations in the demand for surfing equipment, swimwear, snow shovels, and the list goes on. The following graph even suggests a cyclical behavior in employment at securities firms in the United States.^*

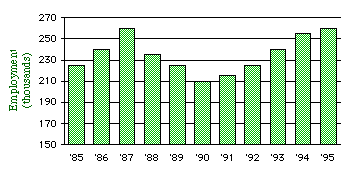
^* Source: Securities Industry Association/The New York Times, September 1, 1996, p. F9.

We model cyclical behavior using the sine and cosine functions. An easy way to describe these functions is as follows. Imagine a bicycle, wheel whose radius is one unit, with a marker attached to the rim of the rear wheel, as shown in the following figure.

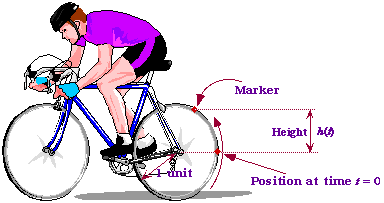As the wheel rotates, the height $h(t)$ of the marker above the center of the wheel, fluctuates between $-1$ and $+1.$ The faster the wheel rotates, the faster the oscillation. Let us now choose our units of measurement so that the wheel has a radius of one unit. Then the circumference of the wheel (the distance all around) is known to be $2\pi,$ where $\pi = 3.14159265....$ When the outer edge of the wheel has traveled this distance, it has gone through exactly one revolution, and so it is back where it started. Thus, if, at time $t = 0$ the marker started off at position $h(0) = 0,$ then it is back to zero after one revolution. If the cyclist happens to be moving at a speed of one unit per second, it will take the bicylce wheel $2\pi$ seconds to make one complete revolution, and so the wheel is back where it started atfer that time.

Press the button to bring up an animation showing $h(t)$ varying with time $t.$

The function $h(t)$ we get in the above way is called the sine function, denoted by $\sin(t).$ Here is its graph.

Sine Function
Bicycle Wheel Definition
If a wheel of radius $1$ unit rotates at a speed of $1$ unit of length per second, and is in the position shown in the figure at time $t = 0,$ then its height after $t$ seconds is given by

$h(t) = \sin(t).$

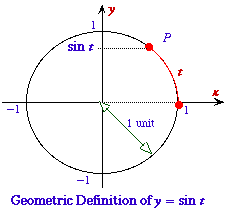
Geometric Definition
The sine of a real number $t$ is given by the $y-$coordinate (height) of the point $P$ in the following diagram, in which $t$ is the distance of the arc shown.
$\sin(t) = y-$coordinate of the point $P.$

Example 1

Using a calculator or a graphing calculator, plot the following pairs of graphs on the same set of axes:

(a)

(b)

(c)

(d)

Solution

(a) The usual graphing calculator format is:

Let us use window coordinates suggested by the graph of $\sin(t)$ shown above, but with larger $y-$coordinates (why?):

The window might look like this:

$Y_1 = \sin(X)$ is shown in red, and $Y_2 = 2*\sin(X)$ in yellow.

We notice that multiplication by $2$ has doubled the amplitude, or distance it oscillates up and down . Wheras the original curve oscillated between $-1$ and $1,$ the new curve oscillates between $-2$ and $2.$ In general:

A $\sin(x)$ has amplitude $A.$

(b) Here, the graphing calculator format is:

Using window coordinates

we get the following:

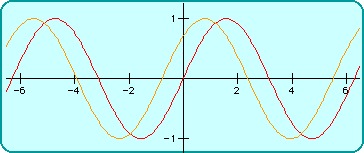$Y_1 = \sin(X)$ is shown in red, and $Y_2 = \sin(X+\pi/4)$ is in yellow.

We notice that addition of $\pi/4$ to the argument has shifted the graph to the left by $\pi/4$ units.In general:

Replacing $x$ by $x+c$ shifts the graph to the left $c$ units.

How would we shift the graph to the right $\pi/4$ units?

(c) Here, the graphing calculator format is:

Using the same window coordinates and color coding as in part (b), we obtain the following graph.

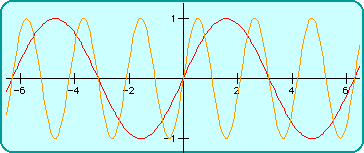Notice that the graph of $\sin(3*x)$ oscillates three times as fast as the graph of $\sin(x).$ Thus, every $2\pi$ units, the graph of $\sin(3*x)$ oscillates three times. In general:

Multiplying $x$ by $b$ multiplies the rate of oscillation by $b.$

(d)

The graphs are shown in the window

Notice several things:

The red graph, $y = \sin(\pix),$ crosses the $x-$axis at integral values $0 ą1, ą2, ...$
For instance, when $x = 1,$ we get $\sin(\pix) = \sin(\pi) = 0.$
The yellow graph, $y = 2\sin(\pi(x+3)),$ is obtained from the red graph by the following two operations:

The following formula illustrates the result of combining some of the operations in the above example.

General Sine Curve

$A$ is called the amplitude (the height of each peak above the baseline)
$C$ is the vertical offset (height of the baseline)
$P$ is the period or wavelength (the length of each cycle)
$ω$ is the angular frequency, given by $ω = 2\pi/P$
$α$ is the phase shift (the horizontal offset of the basepoint; where the curve crosses the baseline as it ascends)

Example 2 Electrical Current^†

The typical voltage V supplied by an electrical outlet in the U.S. is a sinusoidal function that oscillates between $-165$ volts and $+165$ volts with a frequency of $60$ cycles per second. Obtain an equation for the voltage as a function of time $t.$

Solution

What we are looking for is a function of the form

$V(t) = A\sin[ω(t-α)] + C.$

Referring to the above figure, let us look at the constants one-at-a-time.

Amplitude $A$ and Vertical Offset $C:$ Since the voltage oscillates between $-165$ volts and $+165$ volts, we see that $A = 165,$ and $C = 0.$

Period $P:$ Since the electric current oscillates $60$ times in one second, the length of time it takes to oscillate once is $1/60$ second. Thus, the period is $P = 1/60.$

Angular Frequency ω: This is given by the formula

$ω = 2\pi/P = 2\pi(60) = 120\pi.$

Phase Shift $α:$ The phase shift α tells us when the curve first crosses the $t-$axis as it ascends. Since we are not given this information, we can choose $α$ to be an arbitrary number, so let us simply take $α = 0.$

$V(t) = A\sin[ω(t-α)] + C = 165\sin(120\pit),$

where $t$ is time in seconds.

^† See also p. 558 of Calculus Applied to the Real World or p. 1056 of Finite Mathematics and Calculus Applied to the Real World

Example 3 Cyclical Employment Patterns

An economist consulted by your temporary employment agency indicates that the demand for temporary employment (measured in thousands of job applications per week) in your county can be modeled by the function

where $t$ is time in years since January, 1995. Calculate the amplitude, the vertical offset, the phase shift, the angular frequency, and the period, and interpret the results.

Solution

To calculate these constants, first subtract $2\pi$ from the argument (this does not effect the value of the sine function) so that it has the form $4.3\sin(0.82t - n) + 7.3:$

$4.3\sin(0.82t + 0.3) + 7.3 = 4.3\sin(0.82t + 0.3 - 2\pi) + 7.3$

$\approx 4.3\sin(0.82t - 5.983) + 7.3$

Now notice that

and we see right away that $A = 4.3$ (the amplitude), $C = 7.3$ (vertical offset) and $ω = 0.82$ (angular frequency). We also have

$ωα \approx 5.983,$ so that

(rounding to two significant digits; notice that all the terms were given to two digits.) Finally, we get the period using the formula

so that

$P = 2\pi/ω \approx 7.7.$

We can interpret these answers in the form of the following little report:

The demand for termporary employment fluctuates in cycles of $7.7$ years about a baseline of $7\,300$ job applications per week. Every cycle, the demand peaks at $12\,000$ applications per week ($4\,300$ above the baseline) and dips to a low of $3\,000.$ During April, $2002 (t = 7.3)$ the demand for employment was at the baseline level and on an upward cycle.

Section 1 Exercises

2. The Six Trigonometric Functions

Trigonometric Functions Main Page

"RealWorld" Page

Everything for Calculus

We would welcome comments and suggestions for improving this resource.

Mail us at:

Stefan Waner (matszw@hofstra.edu) Steven R. Costenoble (matsrc@hofstra.edu)

The Trigonometric Functions by Stefan Waner and Steven R. Costenoble

This Section: 1. Modeling with the Sine Function

The Trigonometric Functions
by
Stefan Waner and Steven R. Costenoble