Lecture 11: A Little More Relativity: Comoving Frames and Proper Time
11. A Little More Relativity: Comoving Frames and Proper Time
First, we recall some terminology.
|
Definition 11.1 A Minkowskian 4-manifold is a 4-manifold in which the metric has signature (1, 1, 1, -1) (eg., the world according to Einstein).
|
By Proposition 9.2, if M is Minkowskian and m  M, then one can find a locally inertial frame at m such that the metric at m has the form diag(1, 1, 1, -1). We actually have some flexibility: we can, if we like, adjust the scaling of the x4-coordinate to make the metric look like diag(1, 1, 1, -c2). In that case, the last coordinate is the local time coordinate. Later, we shall convert to units of time to make c = 1, but for now, let us use this latter kind of inertial frame.
M, then one can find a locally inertial frame at m such that the metric at m has the form diag(1, 1, 1, -1). We actually have some flexibility: we can, if we like, adjust the scaling of the x4-coordinate to make the metric look like diag(1, 1, 1, -c2). In that case, the last coordinate is the local time coordinate. Later, we shall convert to units of time to make c = 1, but for now, let us use this latter kind of inertial frame.
Note If M is Minkowski space E4, then inertial frames are nothing more than Lorentz frames. (We saw in Theorem 6.3 that Lorentz frames were characterized by the fact that the metric had the form diag(1, 1, 1, -c2) at every point, so they are automatically inertial everywhere.)
Now let C be a timelike curve in the Minkowskian 4-manifold M.
|
Definition 11.2 A momentary comoving reference frame for C (MCRF) associates to each point m  C a locally inertial frame whose last basis vector is parallel to the curve and in the direction of increasing parameter s. Further, we require the frame coordinates to vary smoothly with the parameter of the curve. C a locally inertial frame whose last basis vector is parallel to the curve and in the direction of increasing parameter s. Further, we require the frame coordinates to vary smoothly with the parameter of the curve.
|
|
Proposition 11.3 (Existence of MCRF's)
If C is any timelike curve in the Minkowskian 4-manifold M, then there exists an MCRF for C.
|
Proof
Fix p0  C and a Lorentz frame W(1), W(2), W(3), W(4) of Mp0 (so that
g** = diag(1, 1, 1, -c2).) We want to change this set to a new Lorentz frame V(1), V(2), V(3), V(4) with
C and a Lorentz frame W(1), W(2), W(3), W(4) of Mp0 (so that
g** = diag(1, 1, 1, -c2).) We want to change this set to a new Lorentz frame V(1), V(2), V(3), V(4) with
| V(4) = | dxi

d | | Recall that  = s/c = s/c |
So let us take V(4) as above. Then it is tangent to C at p0. Further,
| ||V(4)||2 = |
  |
dxi

d |
  |
2 |
= |
  |
dxi

ds |
  |
2 |
 |
ds

d |
 |
2 |
= (-1)c2 = -c2. |
using Proposition 6.5. Intuitively, V(4) is the time axis for the observer at p0: it points in the direction of increasing proper time  . We can now invoke Proposition 9.2 to flesh out this orthonormal set to obtain an inertial frame at p0. For the other vectors, take
. We can now invoke Proposition 9.2 to flesh out this orthonormal set to obtain an inertial frame at p0. For the other vectors, take
| V(i) = W(i) + | 2

c2 |
 W(i), V(4) W(i), V(4) V(4) V(4) |
for i = 1, 2, 3. Then
 V(i),V(j) V(i),V(j) | = |
 W(i),W(j) W(i),W(j) + + |
4

c2 |
 W(i),W(4) W(i),W(4)  W(j),W(4) W(j),W(4) + + |
4

c2 |
 W(i),V(4) W(i),V(4)  W(j),V(4) W(j),V(4) ||V(4)||2 ||V(4)||2 |
| = | 0 |
by orthogonality of the W's and the calculation of ||V(4)||2 above. Also,
 V(i),V(i) V(i),V(i) | = |
 W(i),W(i) W(i),W(i) + + |
4

c2 |
 W(i),W(4) W(i),W(4) 2 + 2 + |
4

c2 |
 W(i),V(4) W(i),V(4) 2 ||V(4)||2 2 ||V(4)||2 |
| = | ||W(i)||2 = 1 |
so there is no need to adjust the lengths of the other axes. Call this adjustment a time shear. Since we now have our inertial frame at p0, we can use 9.2 to flesh this out to an inertial frame there.
At another point p along the curve, proceed as follows. For V(4), again use dxi/d (evaluated at p). For the other axes, start by talking W(1), W(2), and W(3) to be the parallel translates of the V(i) along C. These may not be orthogonal to V(4), although they are orthogonal to each other (since parallel translation preserves orthogonality). To fix this, use the same time shearing trick as above to obtain the V(i) at p. Note that the spatial coordinates have not changed in passing from W(i) to V(i)-all that is changed are the time-coordinates. Now again use 9.2 to flesh this out to an inertial frame.
(evaluated at p). For the other axes, start by talking W(1), W(2), and W(3) to be the parallel translates of the V(i) along C. These may not be orthogonal to V(4), although they are orthogonal to each other (since parallel translation preserves orthogonality). To fix this, use the same time shearing trick as above to obtain the V(i) at p. Note that the spatial coordinates have not changed in passing from W(i) to V(i)-all that is changed are the time-coordinates. Now again use 9.2 to flesh this out to an inertial frame.
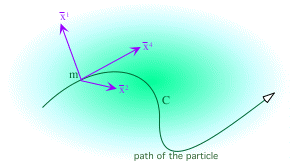 By construction, the frame varies smoothly with the point on the curve, so we have a smooth set of coordinates.
By construction, the frame varies smoothly with the point on the curve, so we have a smooth set of coordinates.
|
Proposition 11.4 (Proper Time is Time in a MCRF)
In a MCRF  , the x4-coordinate (time) is proper time , the x4-coordinate (time) is proper time  . .
|
"Proof"
We are assuming starting with some coordinate system x, and then switching to the MCRF  . Notice that, at the point m,
. Notice that, at the point m,
d 4 4

d |
= |
|
|
= |
  4 4

 xi xi |
V(4)i |
(by definition of V(4)) |
|
|
= |
 4 4
V(4) |
= |
1. (since V(4) has coordinates (0,0,0,1) in the barred system) |
|
In other words, the time coordinate  4 is moving at a rate of one unit per unit of proper time
4 is moving at a rate of one unit per unit of proper time  . Therefore, they must agree.
. Therefore, they must agree.
A particular (and interesting) case of this is the following, for special relativity.
|
Proposition 11.5 (In SR, Proper Time = Time in the Moving Frame)
In SR, the proper time of a particle moving with a constant velocity v is the t-coordinate of the Lorentz frame moving with the particle.
|
Proof
 | = |
s

c |
= |
1

2 |
 |
 |
-gij |
dxi

dt |
dxj

dt |
 |
1/2
|
dt. |
The curve C has parametrization (vt, 0, 0, t) (we are assuming here movement in the x1-direction), and g** = diag (1, 1, 1, -c2). Therefore, the above integral boils down to
 |
= |
|
|
= |
|
|
= |
|
But, by the (inverse)Lorentz transformations:
| t |
= |
|
|
= |

t

(1-v2/c2)1/2 |
since  = 0 for the particle. = 0 for the particle. |
|
Thus,

t |
= |
t(1-v2/c2)1/2 |
= |
 , , |
as required.
|
Definition 11.6 Let C be the world line of a particle in a Minkowskian manifold M. Its four velocity is defined by
| ui | = |
dxi

d |
. |
|
Note By the proof of Proposition 11.3, we have
In other words, four velocity is timelike and of constant magnitude.
Example 11.7 Four Velocity in SR
Let us calculate the four-velocity of a particle moving with uniform velocity v with respect to some (Lorentz) coordinate system in Minkowski space M = E4. Thus, xi are the coordinates of the particle at proper time  . We need to calculate the partial derivatives dxI/d
. We need to calculate the partial derivatives dxI/d , and we use the chain rule:
, and we use the chain rule:
dxi

d |
= |
|
|
= |
| vi |
dx4

d |
for i = 1, 2, 3 |
|
since x4 is time in the unbarred system. Thus, we need to know dx4/d . (In the barred system, this is just 1, but this is the unbarred system...) Since
. (In the barred system, this is just 1, but this is the unbarred system...) Since  4 =
4 =  , we use the (inverse) Lorentz transformation:
, we use the (inverse) Lorentz transformation:
| x4 | = |
 4 + v 4 + v 1/c2 1/c2

(1 - v2/c2)1/2 |
, |
assuming for the moment that v = (v, 0, 0). However, in the frame of the particle,  1 = 0, and
1 = 0, and  4 =
4 =  , giving
, giving
| x4 | = |


(1 - v2/c2)1/2 |
, |
and hence
Now, using the more general boost transformations, we can show that this is true regardless of the direction of v if we replace v2 in the formula by (v1)2 + (v2)2 + (v3)2 (the square magnitude of v). Thus we find
| ui | = |
dxi

d |
= |
vi |
dx4

d |
= |
vi

(1 - v2/c2)1/2 |
(i = 1, 2, 3) |
and
| u4 | = |
dx4

d |
1

(1 - v2/c2)1/2 |
. |
Hence the coordinates of four velocity in the unbarred system are given as follows.
|
Four Velocity in SR
| u* | = | ( v1, v2, v3, 1/ (1-v2/c2)1/2 ) |
|
We can now calculate  u, u
u, u directly as
directly as
 u, u u, u |
= |
| u* |
 |
|
 |
uT |
|
|
= |
v2-c2

(1-v2/c2)1/2 |
= |
-c2. |
|
Special Relativistic Dynamics
If a contravariant "force" field F (such as an electromagnetic force) acts on a particle, then its motion behaves in accordance with
| m0 |
= |
du

d |
= |
F, |
where m0 is a scalar, the rest mass, corresponding to the mass of the particle as measured in its own frame.
We use the four velocity to get four momentum, defined by
Its energy is given by the fourth coordinate, and is defined as
| E | = | c2p4 |
= |
m0c2

(1-v2/c2)1/2 |
. |
Note that, for small v,
| E | = |
m0(1-v2/c2)-1/2 |
 |
m0c2 |
+ |
1

2 |
m0v2. |
In the eyes of a the comoving frame, v = 0, so that
This is called the rest energy of the particle, since it is the energy in a comoving frame.
|
Definitions 11.7 If M is any locally Minkowskian 4-manifold and C is a timelike path or spacelike (thought of as the world line of a particle), we can define its four momentum as its four velocity times its rest mass, where the rest mass is the mass as measured in any MCRF.
|
Exercise Set 10
1. What are the coordinates of four velocity in a comoving frame? Use the result to check that  u, u
u, u = -c2 directly in an MCRF.
= -c2 directly in an MCRF.
2. What can you say about  p, p
p, p , where p is the 4-momentum?
, where p is the 4-momentum?
3. Is energy a scalar? Explain
4. Look up and obtain the classical Lorentz transformations for velocity. (We have kind of done it already.)
5. Look up and obtain the classical Lorentz transformations for mass.
Last Updated: Janyary, 2002
Copyright © Stefan Waner
 M, then one can find a locally inertial frame at m such that the metric at m has the form diag(1, 1, 1, -1). We actually have some flexibility: we can, if we like, adjust the scaling of the x4-coordinate to make the metric look like diag(1, 1, 1, -c2). In that case, the last coordinate is the local time coordinate. Later, we shall convert to units of time to make c = 1, but for now, let us use this latter kind of inertial frame.
M, then one can find a locally inertial frame at m such that the metric at m has the form diag(1, 1, 1, -1). We actually have some flexibility: we can, if we like, adjust the scaling of the x4-coordinate to make the metric look like diag(1, 1, 1, -c2). In that case, the last coordinate is the local time coordinate. Later, we shall convert to units of time to make c = 1, but for now, let us use this latter kind of inertial frame.

 W(i), V(4)
W(i), V(4) V(4)
V(4) , the x4-coordinate (time) is proper time
, the x4-coordinate (time) is proper time 

