Definition 6.1 A smooth inner product on a manifold M is a function  -,- -,-  that associates to each pair of smooth contravariant vector fields X and Y a scalar (field) that associates to each pair of smooth contravariant vector fields X and Y a scalar (field)  X, Y X, Y  , satisfying the following properties. , satisfying the following properties.
|
| Table of Contents | Back to Lecture 5: Tensor Fields | On to Lecture 7: Locally Minkowskian Manifolds: A Little Relativity |
In the last lecture, we saw how the scalar product in Es gave rise to a type (0, 2) covariant tensor field gij. Here, we generalize this concept.
Definition 6.1 A smooth inner product on a manifold M is a function  -,- -,-  that associates to each pair of smooth contravariant vector fields X and Y a scalar (field) that associates to each pair of smooth contravariant vector fields X and Y a scalar (field)  X, Y X, Y  , satisfying the following properties. , satisfying the following properties.
|
Before we look at some examples, let us see how these things can be specified. First, notice that, if x is any chart, and p is any point in the domain of x, then
 X, Y X, Y  | = | XiYj |  |
, |  |
This gives us smooth functions
| gij | = |  |
, |  |
such that
 X, Y
X, Y  = gijXiYj
= gijXiYj
and which, by Proposition 5.3, constitute the coefficients of a type (0, 2) symmetric tensor. We call this tensor the fundamental tensor or metric tensor of the Riemannian manifold.
Examples 6.2
(a) Take M = En, with the usual inner product; we find gij =  ij.
ij.
(b) (Minkowski Metric) M = E4, with gij given by the matrix
| G | = |
|
where c is the speed of light.
Question How does this effect the length of vectors?
Answer We saw in Lecture 3 that, in En, we could think of tangent vectors in the usual way; as directed line segments starting at the origin. The role that the metric plays is that it tells you the length of a vector; in other words, it gives you a new distance formula:
Geometrically, the set of all points in Euclidean 3-space at a distance r from the origin (or any other point) is a sphere of radius r. In Minkowski space, it is a hyperbolic surface. In Euclidean space, the set of all points a distance of 0 from the origin is just a single point; in M, it is a cone, called the light cone. (See the figure.)
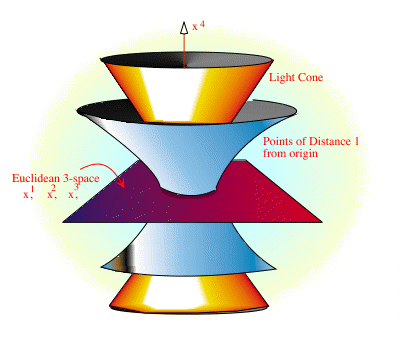
(c) If M is any manifold embedded in Es, then we have seen above that M inherits the structure of a Riemannian metric from a given inner product on Es. In particular, if M is any 3-dimensional manifold embedded in E4 with the metric shown above, then M inherits such a inner product.
(d) As a particular example of (c), let us calculate the metric of the two-sphere M = S2, with radius r, using polar coordinates x1 =  , x2 =
, x2 =  . To find the coordinates of g** we need to calculate the inner product of the basis vectors
. To find the coordinates of g** we need to calculate the inner product of the basis vectors  /
/ x1,
x1,  /
/ x2 in the ambient space Es. We saw in Section 3 that the ambient coordinates of
x2 in the ambient space Es. We saw in Section 3 that the ambient coordinates of  /
/ xi are given by
xi are given by
| j th coordinate | = |  yj yj xi xi |
where
Thus,
  x1 x1 | = | r(cos(x1)cos(x2), cos(x1)sin(x2), -sin(x1)) |
  x2 x2 | = | r(-sin(x1)sin(x2), sin(x1)cos(x2), 0) |
This gives

 /
/ x1,
x1,  /
/ x1
x1  = r2
= r2

 /
/ x2,
x2,  /
/ x2
x2  = r2 sin2(x1)
= r2 sin2(x1)

 /
/ x1,
x1, /
/ x2
x2  = 0,
= 0,
so that
| g** | = |
|
(e) The n-Dimensional Sphere Let M be the n-sphere of radius r with generalized polar coordinates.
(Notice that x1 is playing the role of  and the x2, x3, . . . , xn-1 the role of
and the x2, x3, . . . , xn-1 the role of  .) Following the line of reasoning in the previous example, we have
.) Following the line of reasoning in the previous example, we have
  x1 x1 | = | (-r sin x1, r cos x1 cos x2, r cos x1 sin x2 cos x3 , ... , r cos x1 sin x2... sin xn-1 cos xn, r cos x1 sin x2 ... sin xn-1 sin xn) |
  x2 x2 | = | (0, -r sin x1 sin x2, . . . , r sin x1 cos x2 sin x3... sin xn-1 cos xn, r sin x1 cos x2 sin x3 ... sin xn-1 sin xn) |
  x3 x3 | = | 0, 0, -r sin x1 sin x2 sin x3, r sin x1 sin x2 cos x3 cos x4 . . . , r sin x1 sin x2 cos x3 sin x4... sin xn-1 cos xn, r sin x1 sin x2 cos x3 sin x4 ... sin xn-1 sin xn) |
and so on. This gives

 /
/ x1,
x1,  /
/ x1
x1  = r2
= r2

 /
/ x2,
x2,  /
/ x2
x2  = r2sin2x1
= r2sin2x1

 /
/ x3,
x3,  /
/ x3
x3  = r2sin2x1 sin2 x2
= r2sin2x1 sin2 x2

 /
/ xn,
xn,  /
/ xn
xn  = r2sin2x1 sin2 x2 ... sin2 xn-1
= r2sin2x1 sin2 x2 ... sin2 xn-1
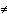 j
j
so that
| g** | = |
|
(f) Diagonalizing the Metric Let G be the matrix of g** in some local coordinate system, evaluated at some point p on a Riemannian manifold. Since G is symmetric, it follows from linear algebra that there is an invertible matrix P = (Pji) such that
| PGPT | = |
|
at the point p. Let us call the sequence (±1,±1, . . . , ±1) the signature of the metric at p. (Thus, in particular, the Minkowski metric has signature (1, 1, 1, -1).) If we now define new coordinates  j by
j by
 j,
j,
 xi/
xi/
 j = Pji, and so
j = Pji, and so
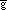 ij ij | = |  xa xa  i i |
gab |  xb xb  j j |
= | PiagabPjb | = | Piagab(PT)bj = (PGPT)ij |
showing that, at the point p,
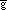 ** ** | = |
|
Thus, in the eyes of the metric, the unit basis vectors ei =  /
/
 i are orthogonal; that is,
i are orthogonal; that is,
 ei, ej
ei, ej  = ±
= ± ij.
ij.
Note The non-degeneracy condition in Definition 6.1 is equivalent to the requirement that the locally defined quantities
are nowhere zero.
Here are some things we can do with a Riemannian manifold.
Definition 6.3 If X is a contravariant vector field on M, then define the square norm norm of X by
 X, X X, X  = gijXiXj. = gijXiXj.
Note that ||X||2 may be negative. If ||X||2 < 0, we call X timelike; if ||X||2 > 0, we call X spacelike, and if ||X||2 = 0, we call X null. If X is not spacelike, then we can define
 |
In the exercise set you will show that null need not imply zero.
Note Since  X, X
X, X  is a scalar field, so is ||X|| is a scalar field, if it exists, and satisfies ||úX|| = |ú|á||X|| for every contravariant vector field X and every scalar field ú. The expected inequality
is a scalar field, so is ||X|| is a scalar field, if it exists, and satisfies ||úX|| = |ú|á||X|| for every contravariant vector field X and every scalar field ú. The expected inequality
 ||X|| + ||Y||
||X|| + ||Y||
need not hold. (See the exercises.)
Arc Length One of the things we can do with a metric is the following. A path C given by xi = xi(t) is non-null if ||dxi/dt||2 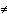 0. It follows that ||dxi/dt||2 is either always positive ("spacelike") or negative ("timelike").
0. It follows that ||dxi/dt||2 is either always positive ("spacelike") or negative ("timelike").
Definition 6.4 If C is a non-null path in M, then define its length as follows: Break the path into segments S each of which lie in some coordinate neighborhood, and define the length of S by
where the sign ±1 is chosen as +1 if the curve is space-like and -1 if it is time-like. In other words, we are defining the arc-length differential form by
|
To show (as we must) that this definition is independent of the choice of chart x, all we need observe is that the quantity under the square root sign, being a contraction product of a type (0, 2) tensor with a type (2, 0) tensor, is a scalar.
|
Proposition 6.5 (Paramaterization by Arc Length)
Let C be a non-null path xi = xi(t) in M. Fix a point t = a on this path, and define a new function s (arc length) by s(t) = L(a, t) = length of path from t = a to t. Then s is an invertible function of t, and, using s as a parameter, ||dxi/ds||2 is constant, and equals 1 if C is space-like and -1 if it is time-like. Conversely, if t is any parameter with the property that ||dxi/dt||2 = ±1, then, choosing any parameter value t = a in the above definition of arc-length s, we have
for some constant C. (In other words, t must be, up to a constant, arc length. Physicists call the parameter |
Exercise Set 6
1. Give an example of a Riemannian metric on E2 such that the corresponding metric tensor gij is not constant.
2. Let aij be the components of any symmetric tensor of type (0, 2) such that det(aij) is never zero. Define
 X, Y
X, Y  a = aijXiYj.
a = aijXiYj.
Show that this is a smooth inner product on M.
3. Give an example to show that the 4. Give an example of a Riemannian manifold M and a nowhere zero vector field X on M with the property that ||X|| = 0. We call such a field a null field.
5. Show that if g is any smooth type (0, 2) tensor field, and if g = det(gij) 6. Suppose that gij is a type (0, 2) tensor with the property that g = det(gij) is nowhere zero. Show that the resulting inverse (of matrices) gij is a type (2, 0) tensor. (Note that it must satisfy gijgkl = 7. (Index lowering and raising) Show that, if Rabc is a type (0, 3) tensor, then Raic given by
8. A type (1, 1) tensor field T is orthogonal in the Riemannian manifold M if, for all pairs of contravariant vector fields X and Y on M, one has
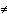 0 for some chart x, then
0 for some chart x, then 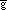 = det(
= det(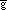 ij)
ij) 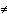 0 for every other chart
0 for every other chart  (at points where the change-of-coordinates is defined). [Use the property that, if A and B are matrices, then det(AB) = det(A)det(B).]
(at points where the change-of-coordinates is defined). [Use the property that, if A and B are matrices, then det(AB) = det(A)det(B).]
 ki
ki lj.)
lj.)
Raic = gibRabc,
is a type (1, 2) tensor. (Here, g** is the inverse of g**.) What is the inverse operation?
where (TX)i = TikXk. What can be said about the columns of T in a given coordinate system x? (Note that the ith column of T is the local vector field given by T( TX, TY
TX, TY =
=  X, Y
X, Y ,
,/
xi).)
Table of Contents
Back to Lecture 5: Tensor Fields
On to Lecture 7: Locally Minkowskian Manifolds: A Little Relativity
Copyright © Stefan Waner