| s(t) | = | t a |
| du | , |
| Table of Contents | Back to Lecture 8: Covariant Differentiation | On to Lecture 10: The Riemann Curvature Tensor |
9. Geodesics and Local Inertial Frames
Let us now apply some of this theory to curves on manifolds. If a non-null curve C on M is paramaterized by xi(t), then we can reparamaterize the curve using arc length,
| s(t) | = | t a |
| du | , |
(starting at some arbitrary point) as the parameter. The reason for wanting to do this is that the tangent vector Ti = dxi/ds is then a unit vector (see the exercises) and also independent of the paramaterization.
If we were talking about a curve in E3, then the derivative of the unit tangent vector (again with respect to s to make it independent of the paramaterization) is a measure of how fast the curve is "turning," and so we call the derivative of Ti the curvature of C.
If C happens to be on a manifold, then the unit tangent vector is still
| Ti | = | ds |
= | dt |
/ | dt |
= |
|
(the last formula is there if you want to actually compute it). But, to get the curvature, we need to take the covariant derivative:
| Pi | = | ds |
||||||
| = | ds |
|||||||
| = | ds2 |
+ | p q |
ds |
ds |
|
Definitions 9.1 The first curvature vector P of the curve C is
A curve on M whose first curvature is zero is called a geodesic. Thus, a geodesic is a curve that satisfies the system of second order differential equations
|
In terms of the parameter t, this becomes (see the exercises)
dt2 |
dt |
- | dt |
dt2 |
+ | p q |
dt |
dt |
dt |
= | 0, |
where
dt |
= |
|
. |
Note that P is a tangent vector at right angles to the curve C which measures its change relative to M.
Question Why is P at right angles to the curve C?
Answer This can be checked as follows.
ds |
 T, T T, T |
= |
|
(Exercise Set 8 #9) | |||||||||
| = |
|
(Symmetry of the scalar product) | |||||||||||
| = |
|
(Definition of P) |
 P, T P, T | = |
|
 T, T T, T | = |
|
(Refer back to the Proof of 6.5 to check this) |
 T, T T, T | = |
|
(Refer back to the Proof of 6.5 to check this) |
Local Flatness, or "Local Inertial Frames"
Notation We will be changing some of the notation to simplify things from now on.
 ijk rather than
ijk rather than  Ti/
Ti/ xk
xk
 Ti/
Ti/ xk etc.
xk etc.
In "flat space" Es all the Christoffel symbols vanish, so the following question arises:
Question Can we find a chart (local coordinate system) such that the Christoffel symbols vanish -- at least in the domain of the chart?
Answer This is asking too much; we shall see later that the derivatives of the Christoffel symbols give an invariant tensor (called the curvature) which does not vanish in general. However, we do have the following.
|
Proposition 9.2 (Existence of a Local Inertial Frame)
If m is any point in the Riemannian manifold M, then there exists a local coordinate system xi at m such that:
We call such a coordinate system a local inertial frame or a normal frame. |
(It follows that  ijk(m) = 0 in an inertial frame.)
ijk(m) = 0 in an inertial frame.)
Before proving the proposition, we need a lemma.
|
Lemma 9.3 (Some Equivalent Things)
Let m (a) gpq,r(m) = 0 for all p, q, r. (b) [pq, r]m = 0 for all p, q, r. (c) |
Proof of Lemma 9.3
(a) 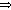 (b) follows from the definition of Christoffel symbols of the first kind.
(b) follows from the definition of Christoffel symbols of the first kind.
(b) 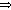 (a) follows from the identity
(a) follows from the identity
gpq,r = [qr, p] + [rp, q] (Check it!)
(b) 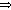 (c) follows from the definition of Christoffel symbols of the second kind.
(c) follows from the definition of Christoffel symbols of the second kind.
(c) 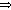 (b) follows from the inverse identity
(b) follows from the inverse identity
[pq, s] = gsrprq.
In other words, the vanishing of Christoffel symbols at any point of M is equivalent to the vanishing of the partial derivatives of the metric tensor at that point.
Click here for a proof of Proposition 9.2.
|
Corollary 9.4 (Partial Derivatives Look Nice in Inertial Frames)
Given any point m  M, there exist local coordinates such that M, there exist local coordinates such that
| ||||||||||||||||||
|
Corollary 9.5 (Geodesics are Locally Straight in Inertial Frames)
If C is a geodesic passing through m  M, then, in any inertial frame, it has zero classical curvature at m (that is, d2xi/ds2 = 0). M, then, in any inertial frame, it has zero classical curvature at m (that is, d2xi/ds2 = 0).
|
Question Is there a local coordinate system such that all geodesics are in fact straight lines?
Answer Not in general; if you make some geodesics straight, then others wind up curved. It is the curvature tensor that is responsible for this. This involves the derivatives of the Christoffel symbols, and we can't make it vanish.
Question If I throw a ball in the air, then the path is curved and also a geodesic. Does this mean that our earthly coordinates are not inertial?
Answer Yes. At each instant in time, we can construct a local inertial frame corresponding to that event. But this frame varies from point to point along our world line if our world line is not a geodesic (more about this below), and the only way our world line can be a geodesic is if we were freely falling (and therefore felt no gravity). Technically speaking, the "earthly" coordinates we use constitute a momentary comoving reference frame; it is inertial at each point along our world line, but the direction of the axes are constantly changing in space-time.
Proposition 9.6 (Changing Inertial Frames)
If x and  are inertial frames at m are inertial frames at m  M, then, recalling that D is the matrix whose ij th entry is ( M, then, recalling that D is the matrix whose ij th entry is ( xi/ xi/  j), one has j), one has
 = ±1. = ±1.
|
Proof By definition of inertial frames,
 ij,
ij,
and similarly for 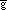 ij, so that
ij, so that 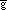 ij = ±gij, whence det(g**) = ± det(
ij = ±gij, whence det(g**) = ± det(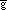 **) = ±1. On the other hand,
**) = ±1. On the other hand,
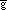 ij ij | = |  xk xk  i i |
 xl xl  j j |
gkl, |
which, in matrix form, becomes
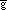 ** = DTg**D.
** = DTg**D.
Taking determinants gives
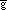 **) = det(DT) det(g**) det(D) = det(D)2 det(g**),
**) = det(DT) det(g**) det(D) = det(D)2 det(g**),
giving
which must mean that det(D)2 = +1, so that det(D) = ±1 as claimed.
Note that the above theorem also workds if we use units in which det g = -c2 as in Lorentz frames.
Definition 9.7 Two (not necessarily inertial) frames x and  have the same parity if det have the same parity if det  > 0. An orientation of M is an atlas of M such that all the charts have the same parity. M is called orientable if it has such an atlas, and oriented if it is equipped with one. > 0. An orientation of M is an atlas of M such that all the charts have the same parity. M is called orientable if it has such an atlas, and oriented if it is equipped with one.
|
Notes
1. Reversing the direction of any one of the axes reverses the orientation.
2. It follows that every orientable manifold has two orientations; one corresponding to each choice of equivalence class of orientations.
3. If M is an oriented manifold and m M, then we can choose an oriented inertial frame
M, then we can choose an oriented inertial frame  at m, so that the change-of-coordinates matrix D has positive determinant. Further, if D happens to be the change-of-coordinates from one oriented inertial frame to another, then det(D) = +1.
at m, so that the change-of-coordinates matrix D has positive determinant. Further, if D happens to be the change-of-coordinates from one oriented inertial frame to another, then det(D) = +1.
4.E3 has two orientations: one given by any left-handed system, and the other given by any right-handed system.
5. In the homework, you will see that spheres are orientable, whereas Klein bottles are not.
We now show how we can use inertial frames to construct a tensor field.
Definition 9.8 Let M be an oriented n-dimensional Riemannian manifold. The Levi-Civita tensor  of type (0, n) is defined as follows. If of type (0, n) is defined as follows. If  is any coordinate system and m is any coordinate system and m M, then define M, then define
 xk/ xk/  l, and where x is any oriented inertial frame at m. l, and where x is any oriented inertial frame at m.
|
Notes
1.
 is a completely antisymmetric tensor. If
is a completely antisymmetric tensor. If  is itself an inertial frame, then, since det(D) = +1 (see Note 2 above) the coordinates of
is itself an inertial frame, then, since det(D) = +1 (see Note 2 above) the coordinates of  (m) are given by
(m) are given by
 i1i2...in(m) i1i2...in(m) |
= | 1, if (i1, i2, ... , in) is an even permutation of (1, 2, ... , n) -1, if (i1, i2, ... , in) is an odd permutation of (1, 2, ... , n) |
2. I have not seen this tensor defined in this generality in any of the sources I consulted. Note that this tensor cannot be defined without a metric being present. In the absence of a metric, the best you can do is define a "relative tensor," which is not quite the same, and what Rund calls the "Levi-Civita symbols" in his book. Wheeler, et al. just define it for Minkowski space.
(Compare this with the metric tensor, which is also "nice" in inertial frames.)
|
Proposition 9.9 (Levi-Civita Tensor)
The Levi-Civita tensor is a well-defined, smooth tensor field. |
Proof To show that it is well-defined, we must show independence of the choice of inertial frames. But, if  and
and  are defined at m
are defined at m M as above by using two different inertial frames, with corresponding change-of-coordinates matrices D and E, then D-E is the change-of coordinates from one inertial frame to another, and therefore has determinant 1. Now,
M as above by using two different inertial frames, with corresponding change-of-coordinates matrices D and E, then D-E is the change-of coordinates from one inertial frame to another, and therefore has determinant 1. Now,
 i1i2...in(m) i1i2...in(m) |
= | det (Di1Di2 ... Din) | |
| = | det D I i1i2...in | ||
| (where I i1i2...in is the identity matrix with columns ordered as shown in the indices) | |||
| = | det D E I i1i2...in E I i1i2...in |
||
(since  E has determinant 1; this being where we use the fact that things are oriented!) E has determinant 1; this being where we use the fact that things are oriented!) |
|||
| = | det E I i1i2...in | (since D = I) = I) |
|
| = |  i1i2...in, i1i2...in, |
||
showing it is well-defined at each point. We now show that it is a tensor. If  and
and  are any two oriented coordinate systems at m and change-of-coordinate matrices D and E with respect to some inertial frame x at m, and if the coordinates of the tensor with respect to these coordinates are
are any two oriented coordinate systems at m and change-of-coordinate matrices D and E with respect to some inertial frame x at m, and if the coordinates of the tensor with respect to these coordinates are
 k1k2...kn and
k1k2...kn and  r1r2...rn = det (Er1Er2 ... Ern) respectively, then at the point m,
r1r2...rn = det (Er1Er2 ... Ern) respectively, then at the point m,
 k1k2...kn k1k2...kn |
= | det (Dk1Dk2 ... Dkn) | |||||||||
| = |
|
||||||||||
(by definition of the determinant(!) since  i1i2...in is just the sign of the permutation!) i1i2...in is just the sign of the permutation!) |
|||||||||||
| = |
|
||||||||||
| = |
|
||||||||||
showing that the tensor transforms correctly. Finally, we assert that det (Dk1Dk2 ... Dkn) is a smooth function of the point m. This depends on the change-of-coordinate matrices to the inertial coordinates. But we saw that we could construct inertial frames by setting
 xi xi  j j |
m |
= | V(j)i, |
where the V(j) were an orthogonal base of the tangent space at m. Since we can vary the coordinates of this base smoothly, the smoothness follows.
Example
In E3, the Levi-Civita tensor coincides with the totally antisymmetric third-order tensor  ijk in Exercise Set 4. In the Exercises, we see how to use it to generalize the cross-product.
ijk in Exercise Set 4. In the Exercises, we see how to use it to generalize the cross-product.
Exercise Set 9
1. Recall that we can define the arc length of a smooth non-null curve by
| s(t) | = | t a |
| du | . |
Assuming that this function is invertible (so that we can express xi as a function of s) show that
ds |
2 | = | ±1. |
2. Derive the equations for a geodesic with respect to the parameter t.
3. Obtain an analogue of Corollary 9.3 for the covariant partial derivatives of type (2, 0) tensors.
4. Use inertial frames argument to prove that gab|c = gab|c = 0. (Also see Exercise Set 3 #1.)
5. Show that, if the columns of a matrix D are orthonormal, then det D = ±1.
6. Prove that, if  is the Levi-Civita tensor, then, in any frame,
is the Levi-Civita tensor, then, in any frame,  i1i2...in = 0 whenever two of the indices are equal. Thus, the only non-zero coordinates occur when all the indices differ.
i1i2...in = 0 whenever two of the indices are equal. Thus, the only non-zero coordinates occur when all the indices differ.
7. Use the Levi-Civita tensor to show that, if x is any inertial frame at m, and if X(1), . . . , X(n) are any n contravariant vectors at m, then
 X(1)| . . . |X(n)
X(1)| . . . |X(n)
is a scalar.
8. The Volume 1-Form (A Generalization of the Cross Product)
If we are given n-1 vector fields X(2), X(3), . . . , X(n) on the n-manifold M, define a covariant vector field by
 X(3)
X(3)  ...
...  X(n))j =
X(n))j =  j i2...inX(2)i2
X(3) i3... X(n) n2,
j i2...inX(2)i2
X(3) i3... X(n) n2,
where  is the Levi-Civita tensor. Show that, in any inertial frame at a point m on a Riemannian 4-manifold, ||X(2)
is the Levi-Civita tensor. Show that, in any inertial frame at a point m on a Riemannian 4-manifold, ||X(2)  X(3)
X(3)  X(4)||2 evaluated at the point m, coincides, up to sign, with the square of the usual volume of the three-dimensional parallelepiped spanned by these vectors by justifying the following facts.
X(4)||2 evaluated at the point m, coincides, up to sign, with the square of the usual volume of the three-dimensional parallelepiped spanned by these vectors by justifying the following facts.
(a) Restricting your attention to Riemannian 4-manifolds, let A, B, and C be vectors at m, and suppose -- as you may -- that you have chosen an inertial frame at m with the property that A1 = B1 = C1 = 0. (Think about why you can you do this.) Show that, in this frame, A B
B C has only one nonzero coordinate: the first.
C has only one nonzero coordinate: the first.
(b) Show that, if we consider A, B and C as 3-vectors a, b and c respectively by ignoring their first (zero) coordinate, then
 B
B C)1 = a.(b
C)1 = a.(b c),
c),
which we know to be ± the volume of the parallelepiped spanned by a, b and c.
9. Define the Levi-Civita tensor of type (n, 0), and show that
(c) Defining ||C||2 = CiCjgij (recall that gij is the inverse of gkl), deduce that the scalar ||A B
B C||2 is numerically equal to square of the volume of the parallelepiped spanned by the vectors a, b and c. (Note also that ||A
C||2 is numerically equal to square of the volume of the parallelepiped spanned by the vectors a, b and c. (Note also that ||A B
B C||2always get the same answer, no matter what coordinate system we choose.)
C||2always get the same answer, no matter what coordinate system we choose.)
 i1i2...in
i1i2...in j1 j2 ... jn
j1 j2 ... jn =
1 if (i1, ... , in) is an even permutation of (j1, ... , jn)
-1 if (i1, ... , in) is an odd permutation of (j1, ... , jn
.
Table of Contents
Back to Lecture 8: Covariant Differentiation
On to Lecture 10: The Riemann Curvature Tensor
Copyright © Stefan Waner